圆:几何学应用
导言
当直线图形与圆关联时,往往具有奇妙的性质。
海伦公式是平面几何中的著名公式,该公式让我们在仅仅已知三角形三边长的情况下求出三角形的面积。古希腊数学家海伦(他曾经活跃在亚历山大教书,故称“亚历山大的海伦”)在公元 60 年出版的《测地术》一书中阐指出,若给定三角形的边长 \(a,b,c\) ,则其面积等于: \[\sqrt{s(s-a)(s-b)(s-c)}\] 其中 \(s\) 是半周长,即 \(s=\dfrac{a+b+c}{2}\)。
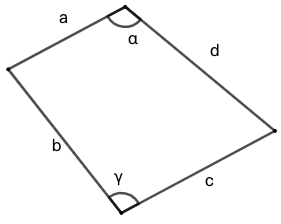
对于圆内接四边形,有一个类似的公式,是印度数学家婆罗摩笈多在公元六世纪提出的。他在《婆罗摩笈多修正体系》一书中指出,圆内接四边形的面积为: \[\sqrt{(s-a)(s-b)(s-c)(s-d)}\]其中 \(a,b,c,d\) 是四边形的边长,\(s\) 依然为半周长 \(\dfrac{a+b+c+d}{2}\) 。
婆罗摩笈多公式是一般(凸)四边形面积公式的特例。若 \(\alpha\) 和 \(\gamma\) 是四边形一对对角的大小,则四边形的面积是是:\[\sqrt{(s-a)(s-b)(s-c)(s-d)-abcd\cdot\cos^2(\dfrac{\alpha+\gamma}{2})}\]
思考与讨论
- 一般四边形面积公式如何导出婆罗摩笈多公式?
- 尝试证明海伦公式(习题);
- 尝试证明一般四边形面积公式(习题);
在以下诸节中,我们通过一系列的经典定理的证明,向读者展示各种基本原理的应用。这些基本原理既包括在“圆”阶段涉及的性质,也包含在“三角形”阶段涉及的性质。
- 托勒密定理:旋转相似、面积公式、梅涅劳斯定理
- 费尔巴哈圆:三角形诸心
- 西姆森定理:三点共线、角度重合法、梅涅劳斯逆定理
- 密克尔定理:圆内接四边形的对角关系
- 帕斯卡定理:梅涅劳斯定理、圆幂定理
- 热尔岗点和纳格尔点:切线长定理、塞瓦定理
托勒密定理
除了面积,圆内接四边形的另一个重要性质就是托勒密定理。克罗狄斯·托勒密(拉丁语:Claudius Ptolemaeus,约90年—168年),是希腊数学家,天文学家,地理学家和占星家。他住在亚历山大,故也称“亚历山大的托勒密”(Claudius Ptolemaeus of Alexandria)。托勒密在《天文学大成》(约公元 150 年出版)中指出:
托勒密定理
一个圆内接四边形的对角线之积等于其两组对边长度乘积之和。即在图 2 所示图形中:\[AC\cdot BD=AB\cdot CD + AD\cdot BC\]
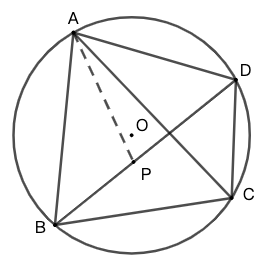
证明一 如图 2 所示,在 \(BD\) 上取点 \(P\) 使得 \(\angle{PAB}=\angle{CAD}\)
\(\because \angle{ABD}=\angle{ACD}\) (\(ABCD\)四点共圆)
\(\therefore \triangle{ABP}\sim\triangle{ACD}\)
\(\therefore AB:AC=BP:CD\) ,即 \(AB\cdot CD=AC\cdot BP\) \(\quad......\)
易证 \(\triangle{ABC}\sim\triangle{APD}\) (旋转相似模型)
有 \(BC\cdot AD=AC\cdot PD\) \(\quad......\)
两式相加,即得
\(AB\cdot CD+BC\cdot AD=AC(BP+PD)=AC\cdot BD\)☐
证明二 如图 3 所示,在 \(AB\) 延长线上取点 \(P\) ,使 \(\angle{PCA}=\angle{DCB}\) 。
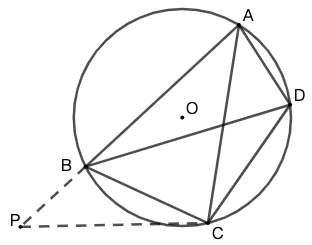
\(\because \angle{PCA}=\angle{DCB},\angle{PAC}=\angle{BDC}\)
\(\therefore \triangle{ACP}\sim\triangle{DCB}\)
\(\therefore AC\cdot BD=CD\cdot AP\) \(\quad......\)
易证 \(\triangle{ACD}=\triangle{PCB}\)
从而 \(AD\cdot BC=CD\cdot PB\) \(\quad......\)
\(-\) 得:
\(AC\cdot BD-AD\cdot BC=CD\cdot(AP-PB)=AB\cdot CD\)
即 \(AC\cdot BC=AB\cdot CD+BC\cdot AD\)☐
点评 我们在之前学习过“相似三角形”,还特别讲述了“相似旋转模型”,这里的证明方法就是构造了该模型。在下两个证明中,我们要运用到三角函数这一强大的工具。
证明三 如图 4 ,做 \(AE\parallel BD\) 交圆 \(O\) 于 \(E\) ,连接 \(EB\) 、\(ED\)。
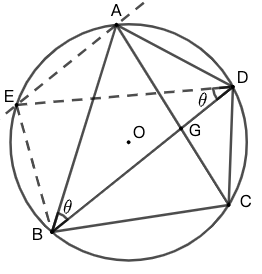
易知 \(BDAE\) 为等腰梯形,
以及 \(EB=AD,ED=AB,\angle{ABD}=\angle{BDE}\)
于是
\(\dfrac{AC\cdot BC}{AD\cdot BC+AB\cdot CD}=\dfrac{AC\cdot BC}{EB\cdot BC+ED\cdot CD}\)
\(=\dfrac{S_{ABCD}:\sin\angle{AGD}}{S_{\triangle{EBC}}:\sin{\angle{EBC}}+S_{\triangle{EDC}}:\sin{\angle{EDC}}}\)
\(\angle{AGD}=\angle{BAC}+\angle{ABD}\) (外角等于两内角和)
\(=\angle{BDC}+\angle{EDB}\) (四点共圆、等腰梯形)
\(=\angle{EDC}=180^\circ-\angle{EBC}\)(内接四边形对角互补)
\(=\dfrac{S_{ABCD}}{S_{\triangle{EBC}}+S_{\triangle{EDC}}}=\dfrac{S_{ABCD}}{{S_{BCDE}}}=1\)☐
证明四 令 \(AB=a, BC=b,CD=c,DA=d,AC=m,BD=n\)
根据余弦定理:
\(m^2=a^2+b^2-2ab\cos\angle{ABC}\) \(\quad......\)
\(m^2=c^2+d^2-2cd\cos\angle{ADC}\)
\(\qquad=c^2+d^2-2cd\cos\angle{ABC}\) \(\quad......\)
由 消去 \(\cos\angle{ABC}\) 得到
\(m=\sqrt{\dfrac{(ac+bd)(ad+bc)}{ab+cd}}\)
类似地
\(n=\sqrt{\dfrac{(ab+cd)(ac+bd)}{ad+bc}}\)
两式相乘得到 \(mn=ac+bd\) ,即为所求证。☐
点评 上述两个证明利用了三角形面积公式和余弦定理。共圆性在这里发挥的关键作用在于其等价命题“四边形对角互补”,望同学们细细体会由共圆带来的角关系,从而带来三角函数值的相等。证明三的辅助线和等积变换,体现了精妙的技巧;证明四则无需任何辅助线,硬算对角线长度,展示了计算的力量。
费尔巴哈圆
1765 年,著名的瑞士数学家 莱昂哈德\(\cdot\)欧拉 证明了三角形的各边中点和三条高的垂足六点共圆。历史上有好几个数学家都曾独立发现过这个圆。在1804年,英国人贝凡 (B.Bevan) 和布特沃尔斯 (J.Butterworth) 已经知道这个圆。1821年,法国数学家布里安双 (C.J.Brianchon, 1783-1864) 和庞斯莱(J.V.Poncelet, 1788-1867)在一篇联名发表的论文中,给出了九点圆的完整证明。德国数学家费尔巴哈 (K.W.Feuerbach, 1800~1834)(这不是那位著名的哲学家)在他的著作中也独立地给出了证明,并给出了关于九点圆的一些奇妙性质,故该圆也常被称为“费尔巴哈圆”。
九点圆定理
三角形的三条高的垂足、三边的中点,以及垂心与顶点的三条连线段的中点,这九点共圆。
即在图 5 中,\(AD,BE,CF\) 是 \(\triangle{ABC}\) 的三条高,垂足分别为 \(D,E,F\) ;\(L,M,N,P,Q,R\) 是所在边或连线段的中点,则 \(D,E,F,L,M,N,P,Q,R\) 九点共圆。
证明提示 首先通过各种中线的平行和长度关系,证明 \(LMPQ\) 为矩形,则 \(P,L\) 在以 \(MQ\) 为直径的圆上。
类似地,\(MNQR\) 也是矩形,从而 \(L,M,N,P,Q,R\) 六点共圆,且矩形的对角线 \(MQ,NR,LP\) 是直径。
又因为 \(\angle{PDL}=09^\circ\) ,所以 \(D\) 也在该圆上。类似地 \(E,F\) 也在该圆上。故 \(D,E,F,L,M,N,P,Q,R\) 九点共圆
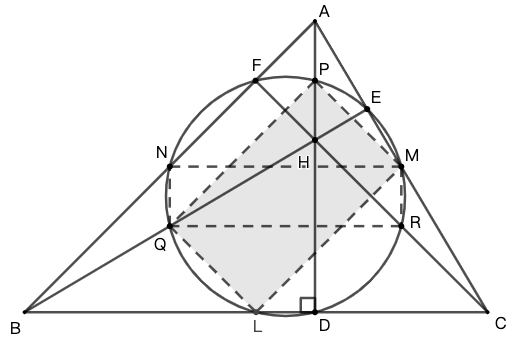
上述证明的完整过程作为习题留给同学。在习题中另有一组关于九点圆的性质及推论。
西姆森定理
西姆森定理刻画了三角形外接圆上一点的有趣性质:从三角形外接圆上一点向三角形三边所做垂线的垂足三点共线。这条线也被称为“西姆森线”。该定理是由苏格兰数学家 威廉\(\cdot\)华莱士 (William Wallace, 1768-1848) 与 1799 年首次提出的。该定理被错误地归功于西姆森,这个错误一直延续至今。
西姆森定理
过三角形外接圆上异于三角形顶点的任意一点做三边的垂线,则三垂足共线。(此线常称为西姆森线)
即在 6 中 \(P\) 是 \(\triangle{ABC}\) 外接圆上一点,\(PL\perp BC, PM\perp AB, PN\perp AC\) ,\(L,M,N\) 为垂足,则 \(L,M,N\) 共线。
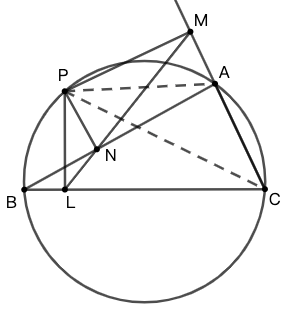
证明一 \(L,M,N\) 共线 \(\quad\Leftarrow\quad\) \(\angle{PMN}=\angle{PML}\)
连接 \(PA,PC\) ,
\(\because \angle{PNA}+\angle{PMA}=180^\circ\)
\(\therefore\) \(P,N,A,M\) 共圆
又 \(\because\) \(A,B,C,P\) 共圆
\(\therefore\) \(\angle{PML}=\angle{PAB}=\angle{PCB}\) \(\quad......\)
又 \(\because\) \(\angle{PMC}+\angle{PLC}=180^\circ\)
\(\therefore\) \(A,B,C,P\) 共圆,\(\angle{PML}=\angle{PCB}\) \(\quad......\)
, \(\quad\Rightarrow\quad\) \(\angle{PML}=\angle{PNL}\) \(\quad\Rightarrow\quad\) \(L,M,N\) 共线☐
梅涅劳斯定理及逆定理
\(\dfrac{BL}{LC}\cdot\dfrac{CM}{MA}\cdot\dfrac{AN}{NB}=\dfrac{PB\cos\angle{PBL}}{PC\cos\angle{PCB}}\cdot\dfrac{PC\cos{\angle{PCM}}}{PA\cos{\angle{PAM}}}\cdot\dfrac{PA\cos{\angle{PAN}}}{PB\cos{\angle{PBN}}}\)
\(\qquad\qquad\qquad\quad=\dfrac{\cos\angle{PBL}}{\cos\angle{PCB}}\cdot\dfrac{\cos{\angle{PCM}}}{\cos{\angle{PAM}}}\cdot\dfrac{\cos{\angle{PAN}}}{\cos{\angle{PBN}}}\)
由共圆性有 \(\angle{PBL}=\angle{PAM},\angle{PCM}=\angle{PBN},\angle{PAN}=\angle{PCB}\)
上述诸余弦纷纷消去,终有 \(\dfrac{BL}{LC}\cdot\dfrac{CM}{MA}\cdot\dfrac{AN}{NB}=1\)
即得 \(L,M,N\) 三点共线。☐
点评 证明三点共线大体上有两种思路,一是直接证明角度的关系,利用重合或平角得出共线结论,如上述证明一;二是将共线转换为共线的等价条件加以证明,如证明二利用的梅涅劳斯定理模型。
密克尔定理
在三角形的辅助下,宇宙间存在这三个圆通过同一个点的关系。这一关系被称为密克尔定理 (Miquel’s theorem) ,它是以法国数学家奥古斯特\(\cdot\)密克尔 (Auguste Miquel, 1816-1851) 的名字命名的。但关于此定理究竟是谁先提出的,尚有疑问。其陈述如下:
密克尔定理
如果在一个三角形的三边上各选取一点,那么有三角形的每个顶点及相邻两边所在直线上的所选两点确定的圆都通过同一公共点。该点称为“密克尔点”。
示例: 如图 7 所示,在 \(\triangle{ABC}\) 的三边 \(BC,CA,AB\) 上各取一点 \(D,E,F\) ,求证圆 \(AEF,BDF,CDE\) 交于一点 \(P\) 。
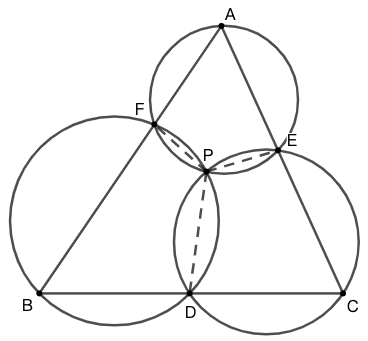
证明 设圆 \(AEF\) 与圆 \(BDF\) 交于点 \(P\) ,连接 \(PD,PE,PF\)。
\(\because\) \(AEPF\) 四点共圆,\(BDPF\) 四点共圆
\(\therefore \angle{CEP}=\angle{AFP}=\angle{BDP}\)
即 \(CDPE\) 四点共圆,也就是说圆 \(CDE\) 也过点 \(P\) 。
于是命题得证。☐
思考与讨论
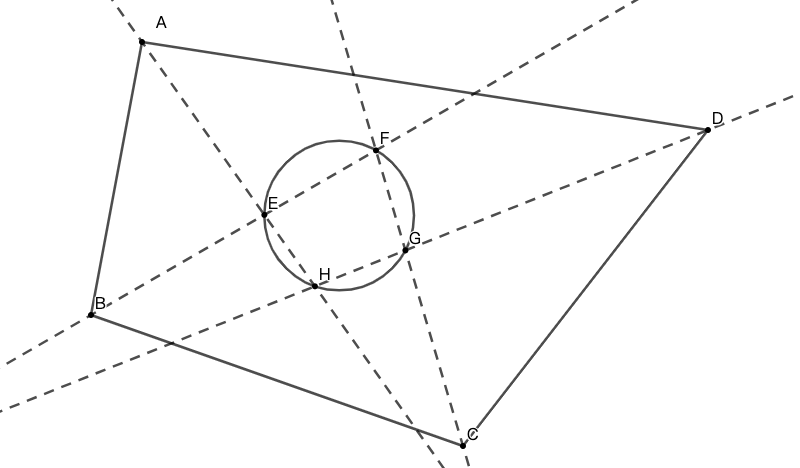
- 事实上,在三角形三边所在直线上(而非线段上)选点,依然有密克尔定理的结论,你能证明之么?
- 如图 8 所示,\(ABC\) 为任意三角形,取 \(F,E,D\) 三点共线,请证明图示四圆共点。(习题)
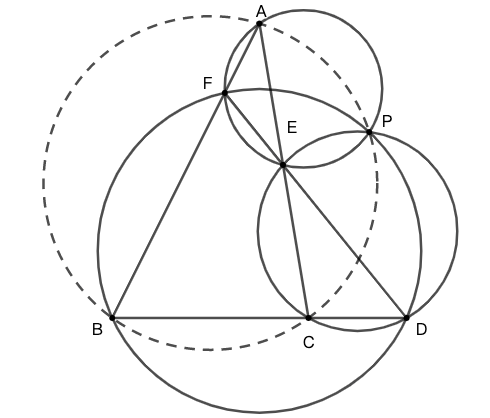
帕斯卡定理
帕斯卡定理
圆的内接六边形的三组对边如果分别相交,那么三个交点共线。(该直线称为帕斯卡线)
即 \(ABCDE\) 内接于圆(该六点无需按次序排列,即无需为凸六边形),直线 \(AB\) 与 \(DE\) 交于点 \(X\) ,直线 \(BC\) 与 \(EF\) 交于点 \(Y\) ,直线 \(CD\) 与 \(FA\) 交于点 \(Z\) ,则 \(X,Y,Z\) 三点共线。
1 这是法国著名数学家布莱兹\(\cdot\)帕斯卡(Blaise Pascal, 1623-1662) 16 岁时发现的一个惊人的定理,发表于 1639 年。帕斯卡本人的证明已经丢失,但在丢失之前莱布尼茨看到过,并称赞过他的证明。帕斯卡喜欢梅涅劳斯定理,故以下运用该定理进行证明。
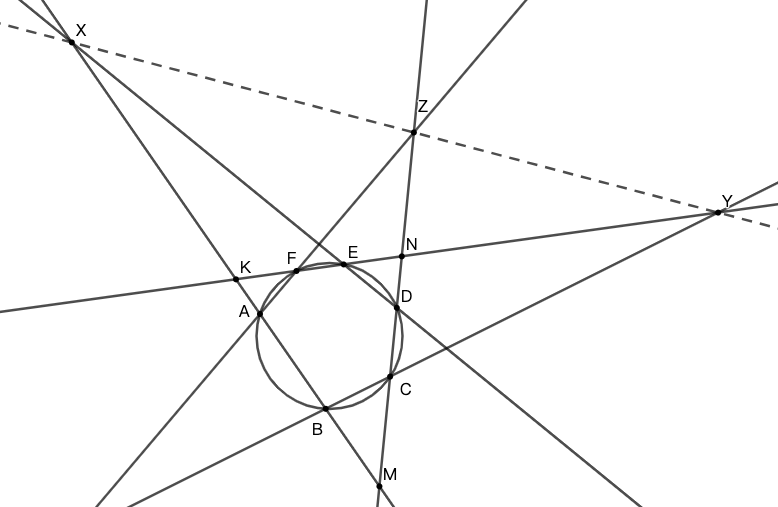
解: 设直线 \(AB\) 与 \(EF\) 交于点 \(K\) ,直线 \(AB\) 与 \(CD\) 交于点 \(M\) ,直线 \(CD\) 与 \(EF\) 交于点 N。
对 \(\triangle{KMN}\) 及截线 \(XED,ZFA,YBC\) 分别应用梅涅劳斯定理
\(\dfrac{NE}{EK}\cdot\dfrac{KX}{XM}\cdot\dfrac{MD}{DN}=1, \dfrac{KA}{AM}\cdot\dfrac{MZ}{ZN}\cdot\dfrac{NF}{FK}=1,\dfrac{MC}{CN}\cdot\dfrac{NY}{YK}\cdot\dfrac{KB}{BM}=1\)
将上述三式相乘,并运用圆幂定理,有
\(MA\cdot MB=MD\cdot MC,ND\cdot NC=NE\cdot NF, KA\cdot KB=KE\cdot KF\)
从而 \(\dfrac{KX}{XM}\cdot\dfrac{MZ}{ZN}\cdot\dfrac{NY}{YK}=1\)
根据梅涅劳斯逆定理,知 \(X,Y,Z\) 三点共线。☐
热尔岗点和纳格尔点
热尔岗点定理
三角形的顶点与其内切圆(或旁切圆)在对边上的切点的连线,三线共点。该点称为“热尔岗点”。
设点 \(D,E,F\) 是 \(\triangle{ABC}\) 的内切圆或一个旁切圆在边 \(BC,CA,AB\) 所在直线上的切点,则 \(AD,BE,CF\) 共点。
该点为法国数学家热尔岗(Gergonne,1771-1859) 所发现。因为一个三角形有一个内接圆和三个旁切圆,所以三角形有四个热尔岗点。
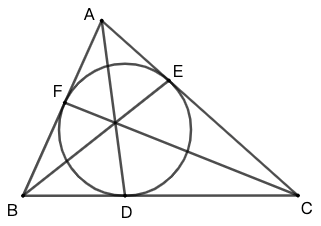
证明 如图 10 所示,根据切线长定理有
\(AE=AF,\quad FB=BD,\quad DC=CE\)
因此,\(\dfrac{AF}{FB}\cdot\dfrac{BD}{DC}\cdot\dfrac{CE}{EA}=1\)
故由塞瓦定理的逆定理,知 \(AD, BE, CF\) 共点。☐
纳格尔点定理
三角形的顶点与其三个旁切圆在对边上的切点的连线,三线共点。该点称为“纳格尔点”。
\(\triangle{ABC}\) 的三个旁切圆分别与边 \(BC,CA,AB\) 相切于点 \(D,E,F\) 则 \(AD,BE,CF\) 共点。
该点为德国数学家纳格尔 (Nagel, 1821-1903) 所发现。由于 \(AD,BE,CF\) 平分三角形的周长,我国学者又将纳格尔点称为第一界心。
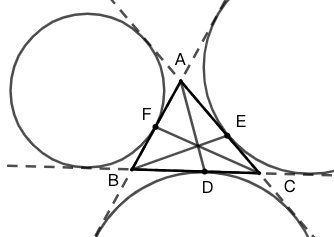
证明 如图 11 所示,设 \(\triangle{ABC}\) 三边分别为 \(a,b,c\) ,\(p=\dfrac{1}{2}(a+b+c)\)
\(\because\) \(AF=p-b=CD\)
\(AE=p-c=BD\)
\(BF=p-a=CE\)
\(\therefore\) \(\dfrac{AF}{FB}\cdot\dfrac{BD}{DC}\cdot\dfrac{CE}{EA}=1\)
有塞瓦定理逆定理可知 \(AD,BE,CF\) 三线共点。☐
点评 塞瓦定理是证明三线共点的重要手段,圆在这里提供了切线的长度信息。
习题
练习: \(\bigstar\)证明海伦公式。
练习: \(\bigstar\)证明婆罗摩笈多公式。
练习: 如图 12 所示,证明任意四边形四条内角平分线的四个交点共圆(相邻两角的平分线的交点)。
练习: 求证,九点圆的圆心是连接三角形垂心 \(H\) 和该三角形外接圆圆心 \(O\) 的线段的中点。
练习: 三角形的外心、重心、九点圆圆心和垂心,依次位于同一直线上,这条直线就叫三角形的欧拉线。求证,外心、重心、垂心三心共线,且外心到重心的距离等于垂心到重心距离的一半。
练习: 如果 \(\triangle{ABC}\) 的高与外接圆相交于点 \(P\) ,那么点 \(P\) 关于 \(\triangle{ABC}\) 的西姆森线平行于圆在点 \(A\) 处的切线 \(AG\) 。
练习: 如图 13 所示,\(ABC\) 为任意三角形,取 \(F,E,D\) 三点共线,请证明图示四圆共点。

练习: 画出三角形旁切圆的热尔岗点,证明对应热尔岗定理。
练习: 证明“弦的塞瓦定理”:如果六个点 \(A,B,C,D,E,F\) 为于同一圆上,那么当且仅当以下等式成立时,弦 \(AD,BE,CF\) 才能通过公共点 \(P\) : \[AB\cdot CD\cdot EF=BC\cdot DE\cdot FA\]