函数基础练习-II
初等函数基础练习
示例: 若 \(a>1,\ b>0\) ,且 \(a^b+a^{-b}=2\sqrt{2}\) ,则 \(a^b-a^{-b}\) 等于
A. \(\sqrt{6}\) \(\qquad\) B. \(2\) 或 \(-2\) \(\qquad\) C. \(-2\) \(\qquad\) D. \(2\)
示例: 若 \(\log{a}\sqrt[5]{b}=c\) 则下列式子正确的是 ( )
A. \(b=a^{5c}\) \(\qquad\) B. \(b^5=a^c\) \(\qquad\) C. \(b=5a^c\) \(\qquad\) D. \(b=c^{5a}\)
示例: 若 \(\log_{5}m-\log_{5}n=a\ (a\in\mathbb{N})\) ,则 \(m\) 是 \(n\) 的 ( )
A. \(a\) 倍 \(\qquad\) B. \(5a\) 倍 \(\qquad\) C. \(5^a\) 倍 \(\qquad\) D. \(5\sqrt{a}\) 倍
示例: 化简 \((\lg2)^2+\lg20\cdot\lg5\) 等于 ( )
A. \(2+\lg^2 2\) \(\qquad\) B. \(4\lg2\) \(\qquad\) C. \(\lg27\) \(\qquad\) D. \(1\)
示例: 化简 \(\log_{\sqrt{2}}2+\log_{27}9+5^{(\log_{\sqrt{5}}\sqrt{3})+1}\) 等于 ( )
A. \(17\dfrac{2}{3}\) \(\qquad\) B. \(17\dfrac{1}{3}\) \(\qquad\) C. \(16\dfrac{2}{3}\) \(\qquad\) D. \(16\dfrac{1}{3}\)
示例: 函数 \(f(x)=\sqrt{a^x-1}\) 的定义域是 \((-\infty,0)\) ,则 \(a\) 的取值范围是 ( )
A. \(a>0\) \(\qquad\) B. \(a>1\) \(\qquad\) C. \(0<a<1\) \(\qquad\) \(a\neq1\)
示例: 函数 \(y=(a^2-1)^x\) 在 \(\mathbb{R}\) 上为减函数,则 \(a\) 的取值范围是
A. \(|a|<1\) \(\qquad\qquad\) B. \(1<|a|<2\)
C. \(1<|a|<\sqrt{2}\) \(\qquad\) D. \(0<|a|<\sqrt{2}\)
示例: 函数 \(y=\left(\dfrac{1}{2}\right)^{x^2-3x+2}\) 的增区间是 ( )
A. \(\left(-\infty,\dfrac{3}{2}\right]\) \(\qquad\) B. \(\left[\dfrac{3}{2},+\infty\right)\) \(\qquad\) C. \([1,2]\) \(\qquad\) D. \((-\infty,0]\cup[1,2]\)
示例: 函数 \(y=\sqrt{\log_{0.5}(x-5)}\) 的定义域是 ( )
A. \((5,+\infty)\) \(\qquad\) B. \((6,+\infty)\) \(\qquad\) C. \((5,6]\) \(\qquad\) D. \((5,6)\)
示例: 函数 \(y=\log_{0.5}(4x-x^2)\) 的值域是 ( )
A. \([-2,+\infty)\) \(\qquad\) B. \(\mathbb{R}\) \(\qquad\) C. \([0,+\infty)\) \(\qquad\) D. \((0,4]\)
示例: 函数 \(y=\log_{x+1}(5-4^x)\) 的定义域是 ( )
A. \((-1,0)\) \(\qquad\) B. \((0,\log_{4}5)\) \(\qquad\) C. \((-1,\log_{4}5)\) \(\qquad\) D. \((-1,0)\cup(0,\log_{4}5)\)
示例: 函数 \(y=\log_{0.5}(x^2-3x+2)\) 的增区间是 ( )
A. \((-\infty,1)\) \(\qquad\) B. \((2,+\infty)\) \(\qquad\) C. \(\left(-\infty,\dfrac{3}{2}\right)\) \(\qquad\) D. \(\left(\dfrac{3}{2},+\infty\right)\)
示例: 函数 \(y=\log_{a}x\) 在 \([2,\pi]\) 上的最大值比最小值大 \(1\) ,则实数 \(a\) 的取值为 ( )
A. \(\dfrac{\pi}{2}\) \(\qquad\) B. \(\dfrac{2}{\pi}\) \(\qquad\) C. \(\dfrac{\pi}{2}\) 或 \(\dfrac{2}{\pi}\) \(\qquad\) D. 不确定
示例: 若 \(\log_{a}\dfrac{3}{4}<1\) ,则 \(a\) 的取值范围是 ( )
A. \(a>1\) \(\qquad\qquad\qquad\) B. \(0<a<\dfrac{3}{4}\)
C. \(a>1\) 或 \(0<a<\dfrac{3}{4}\) \(\qquad\) D. \(a>1\) 或 \(\dfrac{3}{4}<a<1\)
示例: 不等式 \(\log_{\frac{1}{3}}x^2+\log_{3}(x+2)<0\) 的解集为 ( )
A. \((-\infty,-1)\cup(2,+\infty)\) \(\qquad\) B. \((-2,-1)\cup(2,+\infty)\)
C. \((-1,0)\cup(0,2)\) \(\qquad\qquad\) D. \((-2,0)\cup(0,2)\cup(2,+\infty)\)
示例: 若函数 \(y=f(x)\) 是函数 \(y=a^x\ (a>0,a\neq1)\) 的反函数,且 \(f(2)=1\) ,则 \(f(x)=(\ \ \ \ )\)
A. \(\log_{2}x\) \(\qquad\) B. \(\dfrac{1}{2^x}\) \(\qquad\) C. \(\log_{\frac{1}{2}}x\)D. \(2^{x-2}\)
示例: 函数 \(f(x)=(x-3)e^x\) 的单调递增区间是 ( )
A. \((-\infty,2)\) \(\qquad\) B. \((0,3)\) \(\qquad\) C. \((1,4)\) \(\qquad\) D. \((2,+\infty)\)
示例: 已知函数 \(f(x)=\lg\dfrac{1-x}{1+x}\) ,若 \(f(a)=b\) ,则 \(f(-a)=\)
示例: 函数 \(f(x)\) 的定义域为 \(\mathbb{R}\) ,若 \(f(x+1)\) 与 \(f(x-1)\) 都是奇函数,则 ( )
A. \(f(x)\) 是偶函数 \(\qquad\) B. \(f(x)\) 是奇函数
C. \(f(x)=f(x+2)\) \(\qquad\) D. \(f(x+3)\) 是奇函数
示例: 若函数 \(f(x)=x^2+\dfrac{a}{x}\ (a\in\mathbb{R})\) ,则下列结论正确的是
A. \(\forall a\in\mathbb{R}\) , \(f(x)\) 在 \((0,+\infty)\) 是增函数
B. \(\forall a\in\mathbb{R}\) , \(f(x)\) 在 \((0,+\infty)\) 是减函数
C. \(\exists a\in\mathbb{R}\) , \(f(x)\) 是偶函数
D. \(\exists a\in\mathbb{R}\) , \(f(x)\) 是奇函数
示例: 为了得到函数 \(y=\lg\dfrac{x+3}{10}\) 的图像,只需把函数 \(y=\lg x\) 的图像上所有的点 ( )
A. 向左平移 \(3\)各单位长度,再向上平移 \(1\) 个单位长度
B. 向右平移 \(3\)各单位长度,再向上平移 \(1\) 个单位长度
C. 向左平移 \(3\)各单位长度,再向下平移 \(1\) 个单位长度
D. 向右平移 \(3\)各单位长度,再向下平移 \(1\) 个单位长度
示例: 定义在 \(\mathbb{R}\) 上的函数 \(f(x)\) 满足 \(f(x)=\begin{cases}\log_{2}(1-x)\qquad&, x\neq0\\f(x-1)-f(x-2)&, x>0 \end{cases}\) , 则 \(f(2009)\) 的值为 ( )
A. \(-1\) \(\qquad\) B. \(0\) \(\qquad\) C. \(1\) \(\qquad\) D. \(2\)
示例: 设函数 \(f(x)=\dfrac{(x+1)(x+a)}{x}\) 为奇函数,则实数 \(a=\)
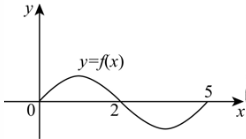
示例: 设奇函数 \(f(x)\) 的定义域为 \([-5,5]\) ,若当 \(x\in[0,5]\) 时, \(f(x)\) 的图像如图所示,则不等式 \(f(x)<0\) 的解是
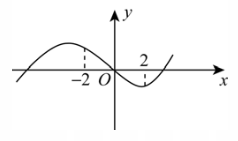
示例: 函数 \(f(x)=ax^3+bx^2+cx+d\) 的图像如图所示,则 \(f(1)+f(-1)\) 的值一定 ( )
A. 等于 \(0\) \(\qquad\) B. 大于 \(0\) \(\qquad\) C. 小于 \(0\) \(\qquad\) D. 小于或等于 \(0\)
示例: 若 \(x\in\mathbb{R},\ n\in\mathbb{N^*}\) ,规定 \(H_x^n=x(x+1)(x+2)...(x+n-1)\) ,
例如:\(H_{-3}^3=(-3)\cdot(-2)\cdot(-1)=-6\) ,则函数 \(f(x)=x\cdot H_{x-3}^7\) :
A. 是奇函数不是偶函数 \(\qquad\) B. 是偶函数不是奇函数
C. 即是奇函数又是偶函数 \(\qquad\) D. 既不是奇函数又不是偶函数
示例: 讨论下列函数的奇偶性
\(f(x)=\lg(x+\sqrt{1+x^2})\) \(\qquad\) (2) \(f(x)=\sqrt{1-x^2}+\sqrt{x^2-1}\)
\(f(x)=\begin{cases}e^x-1(x\geq0)\\1-e^{-x}(x<0)\end{cases}\) \(\qquad\) (4) \(f(x)=\dfrac{\sqrt{1-x^2}}{|x+2|-2}\)
示例: 函数 \(y=\dfrac{ax-1}{x+2}\) 在 \((-2,+\infty)\) 是增函数,实数 \(a\) 的取值范围是 \(\_\_\_\_\_\_\)
示例: 函数 \(f(x)=\log_{0.2}|x+2|\) 的单调增区间是 ( )
A. \((-\infty,-2]\) \(\qquad\) B. \(-(\infty,-2)\) \(\qquad\) C. \((-2,+\infty)\) \(\qquad\) D. \([2,+\infty)\)
示例: 方程 \(\log_{a}x=x-2\ (0<a<1)\) 的解的个数为 ( )
A. \(0\) \(\qquad\) B. \(1\) \(\qquad\) C. \(2\) \(\qquad\) D. \(3\)
示例: 函数 \(f(x)=|2^x-1|\) ,若当 \(a<b<c\) 时有 \(f(a)<f(c)<f(b)\) ,则 ( )
A. \(2^a>2^c\) \(\qquad\) B. \(2^a>2^b\) \(\qquad\) C. \(2^{-a}<2^c\) \(\qquad\) D. \(2^a+2^c<2\)
示例: 函数 \((3^x+1)^{-1}\) 的值域为 \(\_\_\_\_\_\_\)
答案:初等函数基础练习
\(D\) \(\qquad\) 02. \(A\) \(\qquad\) 03. \(C\) \(\qquad\) 04. \(D\) \(\qquad\) 05. \(A\)
\(C\) \(\qquad\) 07. \(C\) \(\qquad\) 08. \(A\) \(\qquad\) 09. \(C\) \(\qquad\) 10. \(A\)
\(D\) \(\qquad\) 12. \(A\) \(\qquad\) 13. \(C\) \(\qquad\) 14. \(C\) \(\qquad\) 15. \(B\)
\(A\) \(\qquad\) 17. \(D\) \(\qquad\) 18. \(-b\) \(\qquad\) 19. \(D\) \(\qquad\) 20. \(C\)
\(C\) \(\qquad\) 22. \(C\) \(\qquad\) 23. \(-1\) \(\qquad\) 24. \((-2,0)\cup(2,5)\)
\(B\) \(\qquad\) 26. \(B\) \(\qquad\) 27. 奇、奇且偶、奇、奇 \(\qquad\) 28. \(\left(-\dfrac{1}{2},+\infty\right)\)
\(B\) \(\qquad\) 30. \(B\) \(\qquad\) 31. \(D\) \(\qquad\) 32. \((0,1)\)
初等函数综合练习
示例: 已知函数 \(f(x)\) 为 \(\mathbb{R}\) 上的减函数,则满足 \(f(\left|\dfrac{1}{x}\right|)<f(1)\) 的实数 \(x\) 的取值范围是 ( )
A. \((-1,1)\) \(\qquad\) B. \((0,1)\) \(\qquad\) C. \((-1,0)\cup(0,1)\) \(\qquad\) D. \((-\infty,-1)\cup(1,+\infty)\)
示例: 在 \(\mathbb{R}\) 上定义的函数 \(f(x)\) 是偶函数,且 \(f(x)=f(2-x)\) ,若 \(f(x)\) 在区间 \([1,2]\) 是减函数,则函数 \(f(x)\) :
A. 在区间 \([-2,-1]\) 上是增函数,区间 \([3,4]\) 上是增函数
B. 在区间 \([-2,-1]\) 上是增函数,区间 \([3,4]\) 上是减函数
C. 在区间 \([-2,-1]\) 上是减函数,区间 \([3,4]\) 上是增函数
D. 在区间 \([-2,-1]\) 上是减函数,区间 \([3,4]\) 上是减函数
示例: 已知定义域为 \(R\) 的函数 \(f(x)\) 在区间 \((8,+\infty)\) 上为减函数,且函数 \(y=f(x+8)\) 为偶函数,则:
A. \(f(6)>f(7)\) \(\qquad\) B. \(f(6)>f(9)\) \(\qquad\) C. \(f(7)>f(9)\) \(\qquad\) D. \(f(7)>f(10)\)
示例: (1) 已知 \(2^{2-a}-2<x<2^{a-2}\) ,函数 \(y=3^x-3^{-x}\) 是奇函数,则实数 \(a=\_\_\_\_\_\_\)
- 已知奇函数 \(f(x)\) 和偶函数 \(g(x)\) 满足 \(f(x)+g(x)=a^x-a^{-x}+2\) 且 \(g(b)=a\) ,则 \(f(a)=\_\_\_\_\_\_\)
示例: 设 \(f(x)\) 是定义在 \(\mathbb{R}\) 上的奇函数,满足 \(f(x+1)=f(x-1)\) ,且已知 \(x\in(0,1)\) 时, \(f(x)=\log_{2}\dfrac{1}{1-x}\) ,则 \(f(x)\) 在 \((1,2)\) 上是 ( )
A. 增函数且 \(f(x)>0\) \(\qquad\) B. 减函数且 \(f(x)>0\)
C. 增函数且 \(f(x)<0\) \(\qquad\) D. 减函数且 \(f(x)<0\)
示例: 将 \(y=2^x\) 的图像 ( ) ,再作关于直线 \(y=x\) 对称的图像,可得函数 \(y=\log_{2}(x+1)\) 的图像。
A. 先向左平移一个单位 \(\qquad\) B. 先向右平移一个单位
C. 先向上平移一个单位 \(\qquad\) D. 先向下平移一个单位
示例: 函数 \(f(x)\) 满足 \(f(x+y)+f(x-y)=2f(x)\cdot f(y)\ (x,y\in\mathbb{R})\) 且 \(f(0)\neq0\) ,试证:\(f(x)\) 是偶函数。
示例: (1) \(7\sqrt[3]{3}-3\sqrt[3]{24}-6\sqrt[3]{1/9}+\sqrt[4]{3\sqrt[3]{3}}\)
- \(\lg5(\lg8+\lg1000)+(\lg2^{\sqrt{3}})^2+\lg\dfrac{1}{6}+\lg0.06\)
示例: 已知 \(f(x)=x^2-x+m\ (m\in\mathbb{R})\) ,
若 \(f(\log_{2}a)=m,\ \log_{2}f(a)=2,\ a\neq1\) ,
求 \(f(\log_{2}x)\) 的最小值及对应的 \(x\) 值;
若 \(f(\log_{2}x)>f(1)\) 且 \(\log_{2}f(x)<f(1)\) ,求 \(x\) 的取值范围。
示例: 已知 \(f(x)=x^2-bx+c,\ f(0)=3\) ,对任意 \(x\) ,恒有 \(f(2-x)=f(x)\) ,试比较 \(f(b^x)\) 与 \(f(c^x)\) 的大小。
示例: \(f(x)\) 是二次项系数小于 \(0\) 的二次函数,且恒有 \(f(2+x)=f(2-x)\) ,求解不等式 \[f[\log_{\frac{1}{2}}(x^2+x+\dfrac{1}{2})]<f[\log_{\frac{1}{2}}(2x^2-x+\dfrac{5}{8})]\]
示例:
若函数 \(f(x)=a^{2x}+2a^x-1\ (a>0,a\neq1)\) 在区间 \([-1,1]\) 上的最大值是 \(14\) ,求 \(a\) 的值;
若函数 \(f(x)=4^xa+2^x+1\) 在 \(x\in(-\infty,1]\) 上 \(f(x)>0\) 恒成立,求 \(a\) 的取值范围。
示例: 设 \(f(x)\) 是定义在 \([-1,1]\) 上的奇函数,且对任意 \(a,b\in[-1,1]\) ,当 \(a+b\neq0\) 时,都有 \(\dfrac{f(a)+f(b)}{a+b}>0\) 。
若 \(a>b\) ,试比较 \(f(a),f(b)\) 的大小;
解不等式 \(f(x-\dfrac{1}{2})<f(x-\dfrac{1}{4})\)
设 \(P={x|y=f(x-c)}\) ,\(Q={x|y=f(x-c^2)}\) 且 \(P\cap Q=\emptyset\) ,求 \(c\) 的取值范围。
答案:初等函数综合练习
\(C\) \(\qquad\) 34. \(B\) \(\qquad\) 35. \(D\) \(\qquad\) 36. (1) \(2\), (2) \(\dfrac{15}{4}\)
\(C\) \(\qquad\) 38. \(D\) \(\qquad\) 39. 略 \(\qquad\) 40. (1) \(0\), (2) \(1\)
- \(\dfrac{7}{4},\sqrt{2}\), (2) \(0<x<1\)
\(f(b^x)\leq f(c^x)\) \(\qquad\) 43. \(\left(1-\dfrac{\sqrt{14}}{4},1+\dfrac{\sqrt{14}}{4}\right)\)