数论初步

数论初步

整除性

整除性是整数的重要性质，它是许多数学分支的基础理论。

整除性（ \(m,n\) 皆为整数）

示例： 奇偶性：如果一个数能够被 \(2\) 整除，那我们就称它为偶数 (even-number) 。不能被 \(2\) 整除的数称为奇数 (odd-number) ，奇数除以 \(2\) 的余数是 \(1\) 。如果 \(n\) 是偶数，那么它一定能写成 \(n=2q\) 的形式，其中 \(q\) 是整数。类似地，奇数 \(n\) 一定能写成 \(n=2q+1\) 的形式。

示例： 判断下列命题的真伪，并简述理由：

思考与讨论

余数

你已经学过带余数的除法\footnote{(何凤波 2014) - 除法 }，下面我们对余数的性质进行深入探讨。

运算的整除性质

对于乘法 \(a\cdot b=c\) 来说，我们关心 \(a,b,c\) 除以同一个数 \(m\) 的余数。

性质 .

如果 \(m\mid a\) ，那么对于任意整数 \(b\) 有 \(m\mid(a\cdot b)\)

这个性质很显然，例如 \(3\mid6\) ，那么任何一个 \(6\) 的倍数都能被 \(3\) 整除。例如 \(6\times11=66\) 而 \(3\mid66\) 。

思考与讨论

示例： 判断以下除法算式能否整除

示例： 判断以下除法算式能否整除

思考与讨论

思考与讨论

运算的余数性质

上面的整除性质是相当显然的，我们还可以得到更一般化的结论，即“求和（乘积）的余数等于余数的求和（乘积）”。

示例： 求 \(7\times14\) 除以 \(3\) 的余数。

解： \(7\) 除以 \(3\) 余 \(1\) ， \(13\) 除以 \(3\) 余 \(2\) 。因此二者乘积除以 \(3\) 的余数为 \(1\times2=2\) 。

☐


很容易验证上述计算的正确性：\(7\times14=98\), \(98\div3=32...2\) 。

在处理大的乘积的余数时，这种方法会立刻显现出它的威力。请看下面的例题：

示例： 求 \(7^{10}\) 除以 \(3\) 的余数。

解： \(7\) 除以 \(3\) 余 \(1\) ，因此 \(7^{10}\) 除以 \(3\) 的余数是 \(1^{10}=1\) 。

☐


请读者自行使用计算器验证这一结论

图 1 展现了上述乘法的余数性质。

7x14

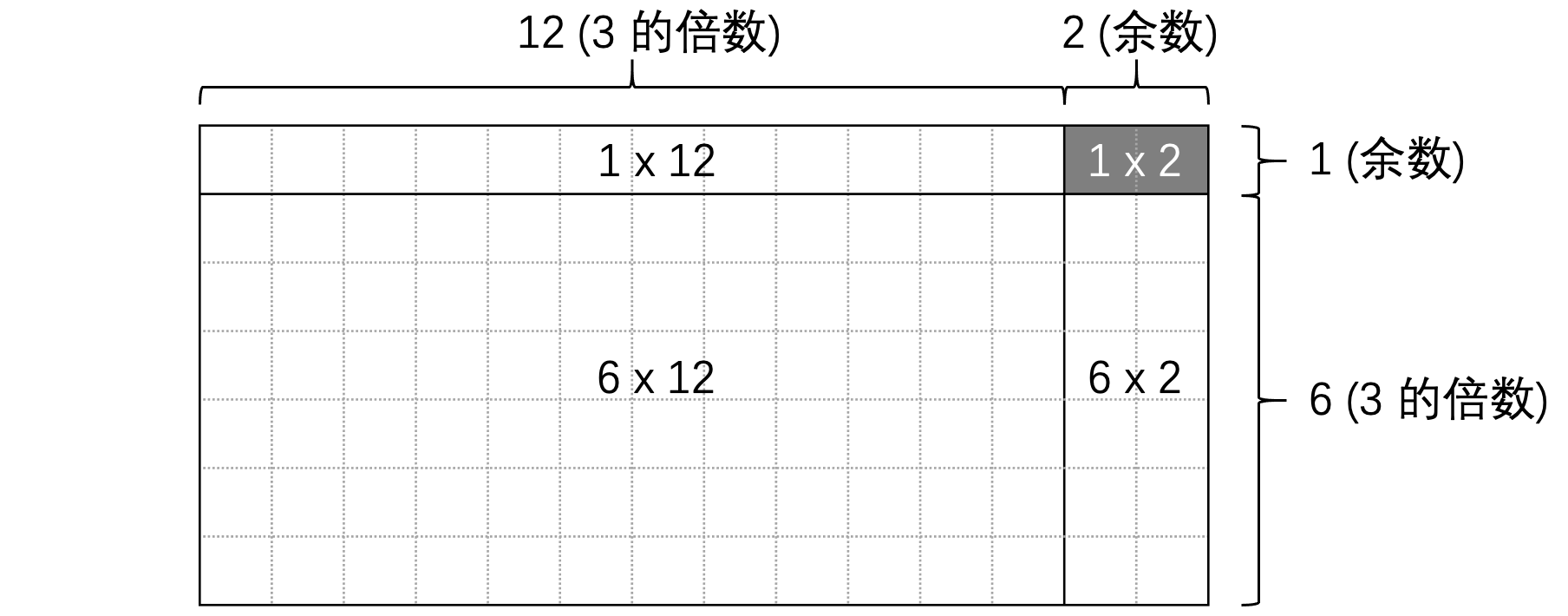
性质 .

如果 \(a\) 除以 \(m\) 的余数为 \(p\) ， \(b\) 除以 \(m\) 的余数是 \(q\) ，则：

[itemsep=0.2em] - \(a+b\) 除以 \(m\) 的余数等于 \(p+q\) 除以 \(m\) 的余数； - \(a\times b\) 除以 \(m\) 的余数等于 \(p\times q\) 除以 \(m\) 的余数；

我们使用 \(a\equiv b \mod m\) 表示 \(a\) 和 \(b\) 除以 \(m\) 有相同的余数，读作“ \(a\) 与 \(b\) 模 \(m\) 同余”。于是上面的关系可以写成如下形式：

性质 .（数学符号表达）

如果 \(a\equiv p \mod m\) 且 \(b\equiv q \mod m\) ： [itemsep=0.2em] - \(a+b\equiv p+q \mod m\)； - \(a\times b\equiv p\times q \mod m\)；；

欧几里得算法

欧几里得算法

为了求出 \(\gcd(a,b)\) ，先令 \(r_{-1}=a, r_0=b\) ，然后相继计算商和余数，\(r_{i-1}=q_{i+1}\cdot r_i+r_{i+1}\) ，直到某余数 \(r_{n+1}=0\) ，则最后的非零余数 \(r_n=\gcd(a,b)\)

欧几里得算法不但可以计算最大公约数，还可以用来求 \(ax+by=\gcd(a,b)\) 的整数解。

示例： 求 \(22x+60y=\gcd(a,b)\) 的一组整数解

线性方程组定理（裴蜀定理）

设 \(a\) 与 \(b\) 是非零整数，\(g=gcd(a,b)\) ，方程 \[ax+by=g\] 总有一个整数解 \((x_1,y_1)\) （可由欧几里得算法得到），方程的通解为 \[\left(x_1+k\cdot\dfrac{b}{g},y_1+k\cdot\dfrac{a}{g}\right)\]

示例： （东大.2019）已知已知 \(n\) 是正整数

  1. 求 \(n^2+1\) 和 \(5n^2+9\) 的最大公约数

  2. 证明 \((n^2+1)(5n^2+9)\) 不是完全平方数

定理： 若 \(p\) 是素数，若 \(p|ab\) ，则 \(p|a\) 或 \(p|b\) 。

证明 若 \(p|a\) 则达成要求，否则 \(gcd(p,a)=1\) ，根据线性方程组定理必定存在整数 \(x,y\) 使得 \[px+ay=1\] 两边同时乘以 \(b\) 得到：\[pbx+aby=b\] \(p\) 整除等式左侧的每一项，所以 \(p|pbx+aby\) ，从而 \(p|b\) 。

☐


定理： 假设素数 \(p\) 整除乘积 \(a_1a_2\cdots a_r\) ，则 \(p\) 至少整除其中至少一个因数。

定理： （算术基本定理）每个整数 \(n\geq2\) 可唯一分解成素数乘积 \(n=p_1p_2\cdots p_r\)

示例： 假设 \(\gcd(a,b)=1\) ，且 \(a|bc\) ，求证：\(a|c\) 。

示例： 假设 \(\gcd(a,b)=1\) ，且 \(a|b, b|c\) 求证 \(ab|c\) 。

示例： 设 \(s,t\) 为奇数， \(s\geq t\geq 1\) 且 \(\gcd(s,t)=1\) 。求证 \(st, \dfrac{s^2-t^2}{2}, \dfrac{s^2+t^2}{2}\) 两两互素。

同余式

同余记号的定义

定义： 若 \(m|a-b\) 记为 \(a\equiv b \mod m\)

性质： 若 \(a_1\equiv b_1 \mod m\) 且 \(\ a_2\equiv b_2 \mod m\)

性质： 若 \(ac\equiv bc \mod m\) 且 \(\gcd(c,m)=1\) ，则 \(a\equiv b \mod m\)

示例： 求证 若 \(ac\equiv bc \mod m\) 且 \(\gcd(c,m)=1\) ，求证 \(a\equiv b \mod m\)

线性同余式定理

定理： 设 \(a,c\) 与 \(m\) 是整数； \(m\geq1\) 且 \(g=\gcd(a,m)\)

如果 \(g\nmid c\) ，则 \(ax\equiv c \mod m\)

如果 \(g\mid c\) ，则 \(ax\equiv c \mod m\) 恰好有 \(g\) 个不同的解：\[x\equiv x_0+k\cdot\dfrac{m}{g} \mod m\] 其中 \(x_0\) 是一个特解。

（求出 \(au+mv=g\) 的特解 \((u_0,v_0)\) ，令 \(x_0=u_0\cdot\dfrac{c}{g}\) 即可）

上述定理的一个推论是以下命题：

性质： 当 \(\gcd(a,m)=1\) 时，线性同余式 \(ax\equiv c \mod m\) 恰有一个解。

示例： 求证：当 \(\gcd(a,m)=1\) 时，线性同余式 \(ax\equiv c \mod m\) 恰有一个解。

示例： 当 \(p\) 为素数时，解同余式 \(x^2\equiv1\mod p\) 。

模 \(p\) 多项式根定理

设 \(p\) 为素数， \(f(x)=a_0x^d+a_1x^{d-1}+a_2x^{d-2}+\cdots+a_d\) 是次数为 \(d\geq1\) 的整系数多项式，且 \(p\nmid a\) 。则 \(f(x)\equiv0\mod p\) 至多有 \(d\) 个模 \(p\) 不同余的解。

证明

费马小定理

设 \(p\) 是素数， \(p\nmid a\) ，则 \(a^{p-1}\equiv1\mod p\)

证明

习题

练习： 使用欧几里得算法计算下列各组数的最大公约数：

  1. \(527,765\)(2) \(361,1178\)(3) \(12321,8658\)

  2. \(108,243\)(3) \(132,473\)(6) \(156,1740\)

练习： 利用欧几里得算法求 \(299\) 和 \(481\) 的最大公约数 \(d\) ，然后求 \(299x+481y=d\) 的一组整数解。

练习： 利用欧几里得算法求 \(129\) 和 \(301\) 的最大公约数 \(d\) ，然后求 \(129x+301y=d\) 的一组整数解。

练习： 求证：正整数 \(a,b\) 的最小公倍数 \(\lcm(a,b)=\dfrac{ab}{\gcd(a,b)}\)

练习： 计算以下各组数的最小公倍数：

  1. \(25,30\) (2) \(42,49\) (3) \(27,81\)

  2. \(28,29\) (5) \(n,n+1\) (6) \(2n-1,2n+1\)

练习： 求证：\(\lcm(ab,ad)=a\cdot \lcm(b,d)\)

练习： 若 \(D=\dfrac{d}{\gcd(b,d)}, B=\dfrac{b}{\gcd(b,d)}\) ，求证： \[\dfrac{a}{b}+\dfrac{c}{d}=\dfrac{aD+cB}{\lcm(b,d)}\]

练习： 求证：\(\gcd(a+b,a-b)\geq\gcd(a,b)\)

练习： 若 \(a,b\) 是非零整数，求证 \(\gcd(a,b)|\lcm(a,b)\)

练习： 令 \(F_m\) 是整数 \(m\) 的倍数的集合，求证：\(F_m\cap F_n=F_{\lcm(m,n)}\)

练习： 求证：(1) \(F_{\gcd(m,n)}\) 包含 \(F_m\) 和 \(F_n\) 的所有元素； (2) 如果 \(F_r\) 包含 \(F_m\) 和 \(F_n\) 的所有元素，那么 \(F_r\) 包含 \(F_{\gcd(m,n)}\) 中的所有元素。

练习： 将“一般斐波那契数列” \(\{a_n\}\) 定义为 \(F_1=a, F_2=b, F_n=c\cdot F_{n-1}+e\cdot F_{n-2}\) ，其中 \(a,b,c,e\) 为整数。

  1. 求证：若 \(d=\gcd(a,b)\) ，则对于全部的 \(n\geq1\) 有 \(d|F_n\) 。

  2. 求证：若 \(f=gcd(F_m,F_{m-1})\) 且 \(\gcd(f,e)=1\) ，则 \(f|d\) 。

练习： 求下列线性丢番图方程的通解：

  1. \(2x+3y=4\) (2) \(17x+19y=23\)

  2. \(15x+51y=41\) (4) \(23x+29y=25\)

  3. \(10x-8y=42\) (6) \(121x-88y=572\)

练习： 某人支付了 \(1.43\) 美元购买苹果和梨。每个苹果 \(17\) 美分，每个梨 \(15\) 美分。他买了多少苹果，多少梨？

练习： 证明顶点在 \((0,0), (b,a)\) 和 \((x,y)\) 的三角形面积等于 \(\dfrac{|by-ax|}{2}\)

练习： 证明如果 \((x_0,y_0)\) 是线性丢番图方程 \(ax-by=1\) 的解，则 \((0,0), (b,a), (x_0,y_0)\) 连成的三角形的面积是 \(1/2\) 。

练习： 是否存在一个顶点在整数格点上的三角形，它的面积小于 \(1/2\) ？证明你的结论。

练习： 直线 \(ax-by=1\) 到原点 \((0,0)\) 的直线距离是多少？

练习： 线性丢番图方程 \(ax+by=c\) 上的最短整点距离（如果存在）是多少？

练习： 证明每个正整数都可以分解为 \(2\) 的非负整数次幂和奇数的乘积。

练习： 利用质因数分解求以下各组数的最大公约数：

  1. \(121,66\)(2) \(169,273\)(3) \(51,187\)

  2. \(2187,999\)(5) \(64,81\)(6) \(p^2q,pqr\) （\(p,q,r\) 均为质数）

练习： 利用质因数分解求以下各组数的最小公倍数：

  1. \(125,150\)(2) \(132,154\)(3) \(39,143\)

  2. \(253,506\)(5) \(111,1221\)(6) \(p^2q,pqr\)（\(p,q,r\) 均为质数）

练习： 如何求多个数的最大公约数和最小公倍数？

练习： 求 \(\gcd(39,102,75)\) 和 \(\lcm(39,102,75)\)

练习： 若 \(d_1=\gcd(a,b), d_2=\gcd(b,c), d_3=\gcd(c,a), D=\gcd(a,b,c)\) ，求 \(\lcm(a,b,c)\)

参考文献

何凤波陈晓梅. 2014. 数学（三年级下册）. 北师大出版社.