三角函数-I:定义和解三角形
三角函数的意义远不止于此
。三角形的基本要素是三条边和三个角,当其中的某些要素确定下来后,整个三角形也就唯一确定了。为了计算这个确定三角形的其余要素(边长和角度),就需要用到三角函数。
在历史上,数学家们首先通过研究直角三角形得到了三角函数的概念,用以刻画直角三角形各边之间的比例。通过制订好的三角函数表,工程师可以很容易地解任意三角形,从而解决诸如计算建筑物高度之类的问题。
函数概念的复习
如二次函数,三角函数也是函数,我们来回顾一下函数的定义。下文整理自百度百科《函数》词条
函数这一概念最早由中国清朝数学家李善兰翻译,出于其著作《代数学》:“凡此变数中函彼变数者,则此为彼之函数”。意思是,函数指一个量随着另一个量的变化而变化,或者说一个量中包含另一个量。这实际上是函数最朴素的定义。
传统定义(人教版初中课本)
定义: 在一个变化过程中,发生变化的量叫变量,有些数值是不随变量而改变的,我们称它们为常量。
自变量(x):一个与它量有关联的变量,这一量中的任何一值都能在它量中找到对应的固定值。
因变量(y):随着自变量的变化而变化,且自变量取唯一值时,因变量有且只有唯一值与其相对应。
函数关系:上述因变量和自变量之间的关系称为函数关系。 \(x\) 确定一个值,\(y\) 就随之确定一个值。当 \(x\) 取 \(a\) 时, \(y\) 就随之确定为 \(b\), \(y_1\) 就叫做 \(x_1\) 的函数值。
集合、映射和函数
定义: 设 \(X\) 和 \(Y\) 是两个非空集合,如果按照某种对应关系,对于集合 \(X\) 中的任何一个元素,在集合 \(Y\) 中都存在唯一的元素与之对应,那么这样的对应叫做集合 \(A\) 到集合 \(B\) 的映射。定义在非空数集之间的映射称为函数。
概念辨析
在我国现行中学教材中,映射是在集合间定义的,而函数是在数集(实数集)之间定义的。函数是一种特殊的映射。
如果读者阅读更广泛的数学教材,会发现映射和函数这两个字眼的区分有时不是那么清晰,有些著作以“映射”作为统一名称,有的著作则使用“函数”字眼。
函数、定义域和值域(人教版高中课本必修一)
定义: 一般地,设 \(A,B\) 是非空的实数集,如果对于集合 \(A\) 中的任意一个数 \(x\) ,按照某种确定的对应关系 \(f\) ,在集合 \(B\) 中都有唯一确定的数 \(y\) 和它对应,那么就称 \(f:A\mapsto B\) 为从集合 \(A\) 到集合 \(B\) 的一个函数,记作 \[y=f(x), x\in A\] 其中,\(x\) 叫做自变量, \(x\) 的取值范围 \(A\) 叫做函数的定义域;与 \(x\) 的值对应的 \(y\) 值叫做函数值,函数值的集合 \({f(x)|x\in A}\) 叫做函数的值域。
示例: 请指出等差数列 \(1,3,5,7,9,...\) (无穷多项),在项数和项之间建立的函数关系:
- 传统定义语言:
- 自变量:\(n=1,2,3,4,5,...\)
- 因变量:\(a_n=1,3,5,7,9,...\)
- 函数关系:\(a_n=2n-1\)
- 集合映射语言:
- 集合 \(A\):正整数集合 \(N^+\)
- 集合 \(B\):实数集合 \(R\)
- 映射关系 \(f\):\(y=f(x)=2x-1, x\in N^+\)
☐
示例: 请指出函数 \(f(x)=x^2\) 的定义域和值域。
示例: 请指出函数 \(f(x)=x^2+2x , x\in[-2,2]\) 的值域。
示例: 请指出函数 \(f(x)=\dfrac{x+1}{x-1}\) 的定义域和值域。
锐角三角函数的定义
1 三角函数是角的度量函数,它把三角形的角与它的边长联系起来,并且有许多其它的应用。对于锐角 \(\theta\) ,我们定义如下的三角函数:
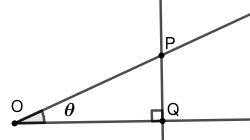
锐角三角函数的定义(直角三角形)
如图 1 所示,令 \(\angle{O}=\theta\) ,在角的一边上取点 \(P\) (与 \(O\) 不重合) ,做 \(PQ\) 垂直于另一边,垂足为 \(Q\) 。我们定义正弦(\(\sin\))、余弦(\(\cos\))、正切(\(\tan\))函数如下: \[\sin \theta = \dfrac{|PQ|}{|OP|}\quad,\quad \cos \theta = \dfrac{|OQ|}{|OP|}\quad,\quad \tan \theta = \dfrac{|PQ|}{|OQ|}\]
定义上述诸函数的倒数为余割(\(\csc\))、正割(\(\sec\))、余切(\(\cot\))函数: \[\csc \theta = \dfrac{|OP|}{|PQ|}\quad,\quad \sec \theta = \dfrac{|OP|}{|OQ|}\quad,\quad\cot \theta = \dfrac{|OQ|}{|PQ|}\]
示例: 证明上述定义中,三角函数值与 \(P\) 点的选择无关。
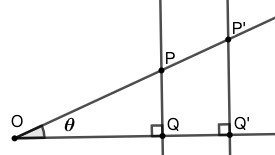
示例: 根据三角函数的定义,计算 \(\sin30^\circ\) 、 \(\cos30^\circ\) 、\(\tan30^\circ\)
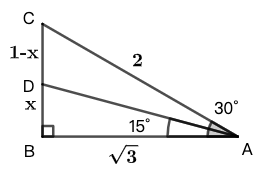
示例: 表 3 给出最常用的锐角三角函数。
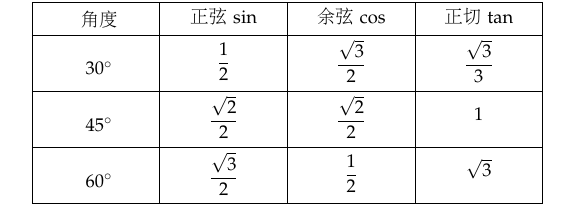
思考与讨论
- 观察上表中的三角函数值,你能发现什么规律?
- 用计算器验证你发现的规律。你能证明你发现的规律么?
- 你应当如何定义 \(0^\circ\) 和 \(90^\circ\) 的三角函数?
示例: 观察图 4 当点 \(B\) 向下运动到无限接近 \(C\) 点时,\(\angle{A}\) 无限接近 \(0^\circ\) ,\(\angle{B}\) 无限接近 \(90^\circ\) ,给出此时两角的三角函数值。
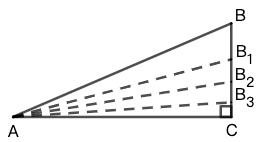
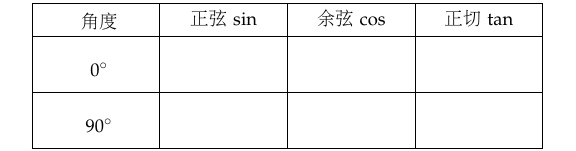
示例: 求 \(\sin15^\circ\) (提示:使用角平分线定理)。
对于锐角三角函数,以下性质是容易证明的:2
三角函数的性质(余角的三角函数)
性质: \(\sin\alpha=\cos(90^\circ-\alpha)\)
性质: \(\tan\alpha=\cot(90^\circ-\alpha)\)
性质: \(\sec\alpha=\csc(90^\circ-\alpha)\)
作者按:这其实正是“余弦”、“余切”里面“余”字的由来。正弦值等于“余”角的“余”弦值,正切值等于“余”角的“余”切值。
三角函数的性质(同角的三角函数)
性质: \(\sin^2\alpha+\cos^2\alpha=1\)
性质: \(\tan\alpha=\dfrac{\sin\alpha}{\cos\alpha}\)
作者按:同角三角函数的“性质”还有很多,但这些性质往往可以很容易得到,例如 \[\tan\alpha\cdot\cot\alpha=1,\quad 1+\tan^2\alpha=\sec^2\alpha\] 其余种种,不一而足。请见如下例题
示例: 已知 \(\tan\alpha=\dfrac{3}{4}\) ,利用上述性质求锐角 \(\alpha\) 的各三角函数值。 (\(\cot,\sin,\cos,\sec,\csc\))
示例: 已知 \(\sin15^\circ=\dfrac{\sqrt{6}-\sqrt{2}}{4}\) ,利用上述性质求 \(15^\circ\) 角的各三角函数值。 (\(\tan,\cot,\cos,\sec,\csc\))
示例: 有了上述性质,再配合先前通过几何方法计算得到的 \(\sin15^\circ\) ,可以得到表 所示三角函数表。

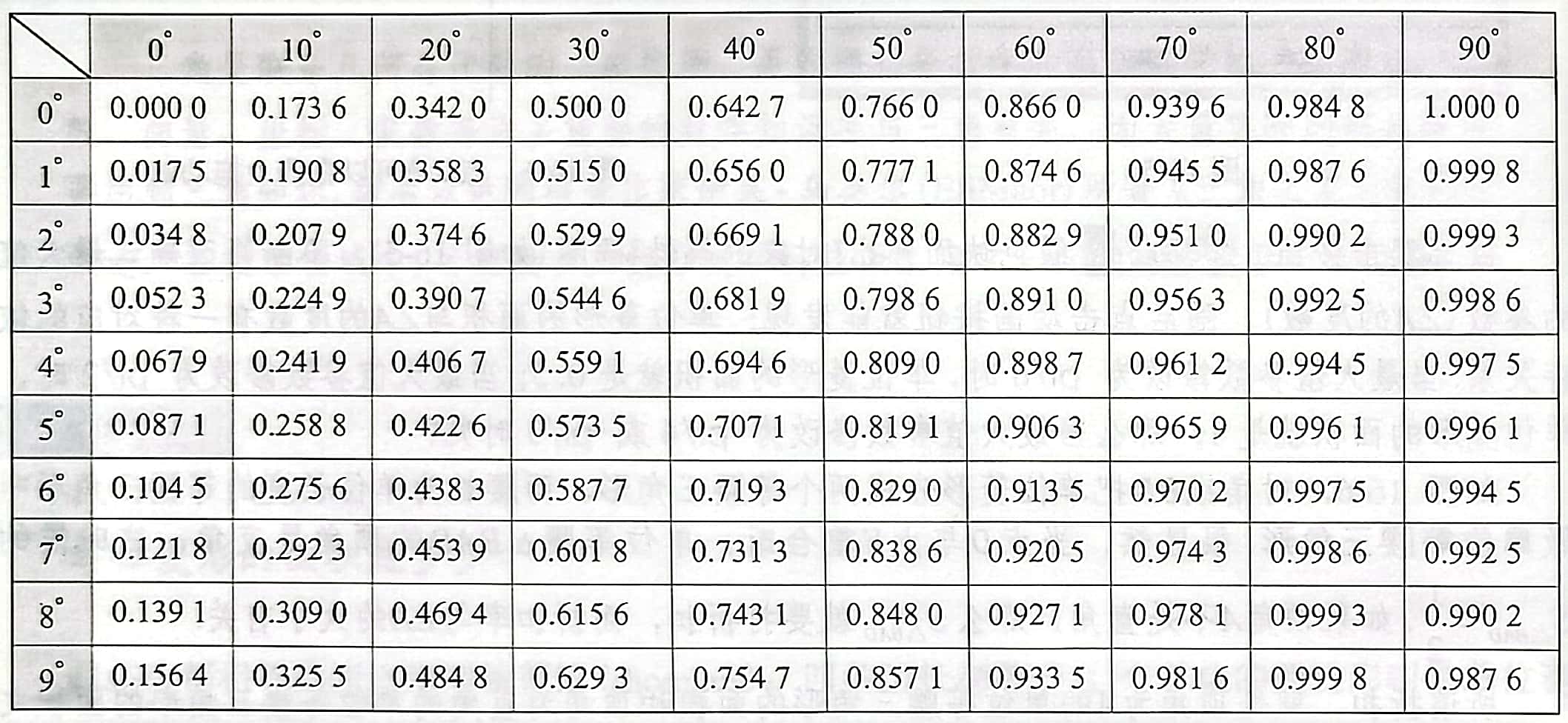
示例: 在 \(Rt\triangle{ABC}\) 中,\(\angle{C}=90^\circ\),\(AB=5\), \(BC=1\) ,使用如下三角函数表计算 \(\angle{A}\) 的度数。3
三角函数的几何应用
三角形的面积公式
三角形面积公式
定理: \(\triangle{ABC}\) 的三个角分别为 \(\angle{A},\angle{B},\angle{C}\) ,三个角所对的边的长度分别为 \(a,b,c\) 则\(\triangle{ABC}\) 的面积计算公式如下:\[S_{\triangle{ABC}}=\dfrac{1}{2}ab\sin{\angle{C}}=\dfrac{1}{2}bc\sin{\angle{A}}=\dfrac{1}{2}ca\sin{\angle{B}}\] 即:三角形面积等于两边之积乘以夹角的正弦值再除以二。
请注意,我们只定义了锐角的三角函数,但是当我们将三角函数扩展至钝角后,针对钝角三角形仍有相同公式,故此处不做特殊说明。
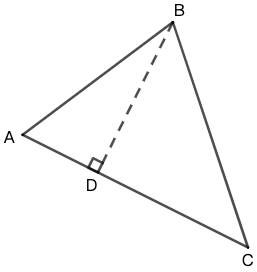
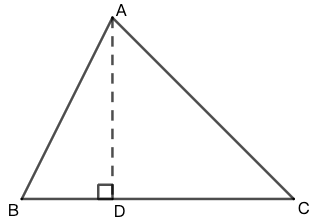
示例: 证明上述三角形面积公式,参考图如图 9 所示。
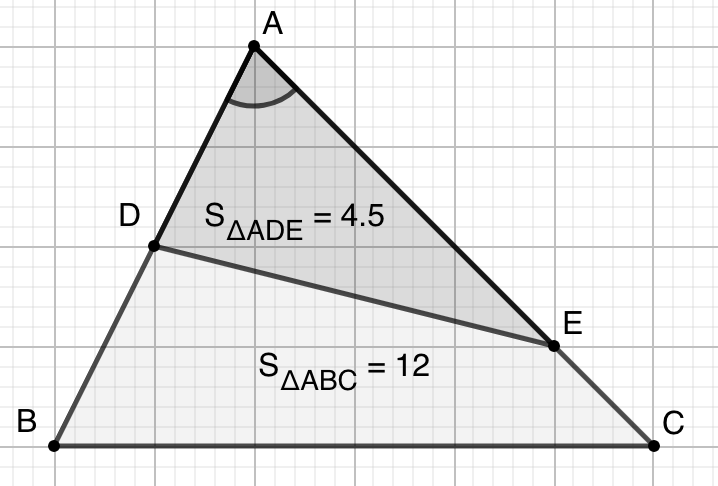
示例: 鸟头模型:在任意 \(\triangle{ABC}\) 中 \(D\) 、 \(E\) 分别 \(AB\) 、\(AC\) 边上两点,如图 10 所示。则三角形的面积之比满足: \[\dfrac{S_{\triangle{ADE}}}{S_{\triangle{ABC}}}=\dfrac{|AD|\cdot|AE|}{|AB|\cdot|AC|}\]
思考与讨论
- 如果在图 9 中 \(\angle{A}\) 是钝角,也有类似的鸟头模型结论么?
- 如果两个三角形的一角互补而不是相等,也有类似鸟头模型的结论,你能叙述该结论么?
- 你能证明上述结论么?
- 通过“钝角/补角鸟头模型”,你认为应当如何定义钝角的正弦值?
☐
在研究四直线相交截线段比例时,我们介绍过角平分线定理:三角形的内角平分线分对边的线段之比等于两邻边之比。在三角函数的加持下,我们可以突破“角平分线”的限制,得出更一般的结论。
角分线定理(比例引理)
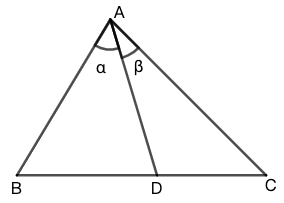
定理: 在 \(\triangle{ABC}\) 中 \(D\) 是 \(BC\) 边上一点。\(AD\) 分 \(\angle{BAC}\) 的角度为 \(\alpha\) 和 \(\beta\) 。则 \(D\) 分线段 \(BC\) 之比为: \[\dfrac{|BD|}{|DC|}=\dfrac{|AB|\cdot \sin\alpha}{|AC|\cdot \sin\beta}\]
示例: 使用三角形面积公式,证明角分线定理。
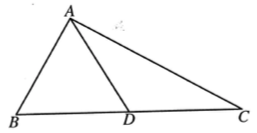
示例: 如图 12 所示,在 \(Rt\triangle{ABC}\) 中,\(\angle{BAC}=90^\circ\),点 \(D\) 在 \(BC\) 上, \(\angle{BAD}=60^\circ\) ,\(AB=CD\) 。求证 \(\angle{C}=30^\circ\) 。
正弦函数的延拓
三角形的角除了锐角外,还有直角和钝角。为了能处理一般的三角形,我们需要将锐角三角函数的定义拓展至 \(0 - 180^\circ\) 。
延拓的概念
设 \(E\) 与 \(F\) 为两个集合, \(P\) 为 \(E\) 的子集,而 \(f\) 为从 \(P\) 到 \(F\) 中的映射. 任一从 \(E\) 到 \(F\) 中的映射,如果它在 \(P\) 上的限制为 \(f\) ,则称该映射为 \(f\) 在 \(E\) 上的延拓。 《百度百科-延拓》
简而言之,延拓就是在扩展定义域的同时保证原有定义域的计算结果不变。例如我们将自然数的四则运算扩展至有理数和实数,就是从 \(f:N\times N\mapsto R\) 到 \(f:R\times R\mapsto R\) 的延拓。当拓展某个函数的定义域时,明智的选择是尽量保持原有函数的性质。借用电子产品软件升级时的常用说法,就是在功能升级的同时提供“向下兼容性”。
到目前为止,关于正弦函数最重要的应用就是三角形面积公式 \[S_{\triangle{ABC}}=\dfrac{1}{2}bc\sin\angle{A}\]
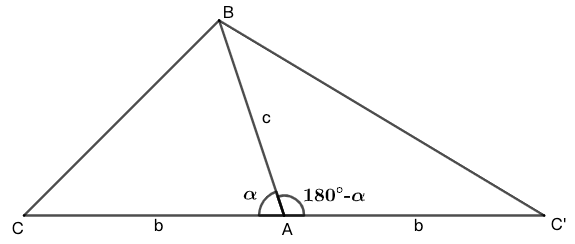
我们希望将正弦函数延拓至 \(0-180^\circ\) ,同时保持该公式成立。为此考虑图 13 所示的情形:图中,\(AC=AC'\),\(\angle{BAC}+\angle{BAC'}\) 。 \[S_{\triangle{ABC'}}=S_{\triangle{ABC}}=\dfrac{1}{2}bc\sin\alpha\]
钝角的正弦函数值
钝角的正弦函数值
定义: \(\sin\alpha=\sin(180^\circ-\alpha)\)
从而 \[S_{\triangle{ABC'}}=\dfrac{1}{2}bc\sin(180^\circ-\alpha)=\dfrac{1}{2}bc\sin\alpha=S_{\triangle{ABC}}\]
正弦定理
本节讨论一个三角形中非常基础的定理“正弦定理”。该定理建立了三角形三边与角度正弦值的比例关系。
正弦定理
定理: 在 \(\triangle{ABC}\) 中 \(\angle{A}, \angle{B}, \angle{C}\) 对应的边分别为 \(a,b,c\) \[\dfrac{a}{\sin\angle{A}}=\dfrac{b}{\sin\angle{B}}=\dfrac{c}{\sin\angle{C}}\]
事实上,这个比值等于三角形外接圆的直径 \(2R\) 。
示例: 验证正弦定理。
示例: 证明正弦定理。(注意讨论你的证明是否针对各种三角形都成立)
余弦定理
正弦定理告诉我们比例,而余弦定理告诉我们那条边到底有多长。
余弦定理
定理: 在 \(\triangle{ABC}\) 中 \(\angle{A}, \angle{B}, \angle{C}\) 对应的边分别为 \(a,b,c\) \[a^2=b^2+c^2-2bc\sin\angle{A}\]
三角形的三边处于对称地位,所以 \(a,b,c\) 是可以轮换的,所以同时也有以下关系 \[b^2=c^2+a^2-2ca\cos\angle{B}\] \[c^2=a^2+b^2-2ab\cos\angle{C}\]
示例: 验证余弦定理。

钝角三角形的证明,留做作业

我们通过定义钝角的正弦值等于其补角的正弦值,从而获得了三角形面积公式和正弦定理的统一表述形式。应当如何定义钝角的余弦函数值,从而获得统一的余弦定理表述形式呢?
示例: 证明若 \(b\) 是一个三角形中钝角的对边,则 \[b^2=a^2+c^2+2ac\cos\angle{B'}\] 其中 \(B'\) 是钝角 \(B\) 的补角。4
基于这个结果,我们给出 钝角的余弦值的定义:
钝角的余弦值
定义: 一个钝角的余弦等于其补角的余弦乘以 \(-1\) 。进一步,对于 \(\alpha\in[0^\circ,180^\circ]\) 有:\[\cos\alpha=-\cos(180^\circ-\alpha)\]
从而得到余弦定理的统一形式 \(b^2=c^2+a^2-2ca\cos\angle{B}\) 。
示例: 在图 18 所示的钝角三角形中验证余弦定理。
基础练习:三角函数的定义
练习: 若一个三角形的三条边边长分别由下面各组数给出,试判断该三角形试锐角、直角还是钝角三角形。(提示:使用勾股定理)5
\(\{6,7,8\}\) (2) \(\{6,8,10\}\) (3) \(\{6,8,9\}\) (4) \(\{6,8,11\}\)
\(\{5,12,12\}\) (6) \(\{5,12,14\}\) (7) \(\{5,12,17\}\)
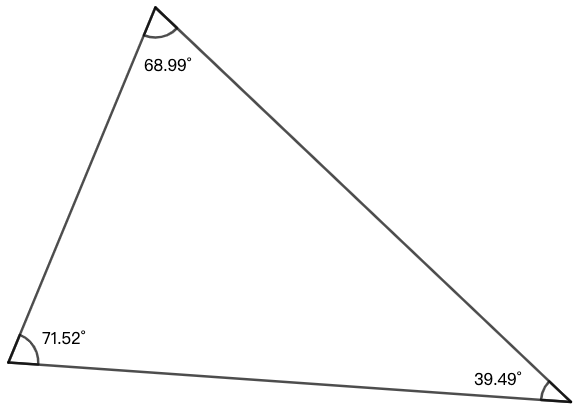
练习: 写出图 19 中 角 \(\alpha\) 和 \(\beta\) 的正弦值。6

练习: 仅使用直尺和圆规,绘制正弦值为 \(\dfrac{2}{3}\) 的锐角。并叙述作图过程。7
练习: 仅使用直尺和圆规,绘制余切值为 \(2\) 的锐角。并叙述作图过程。8
练习: 仅使用直尺和圆规,绘制正割值为 \(\dfrac{4}{3}\) 的锐角。并叙述作图过程。9
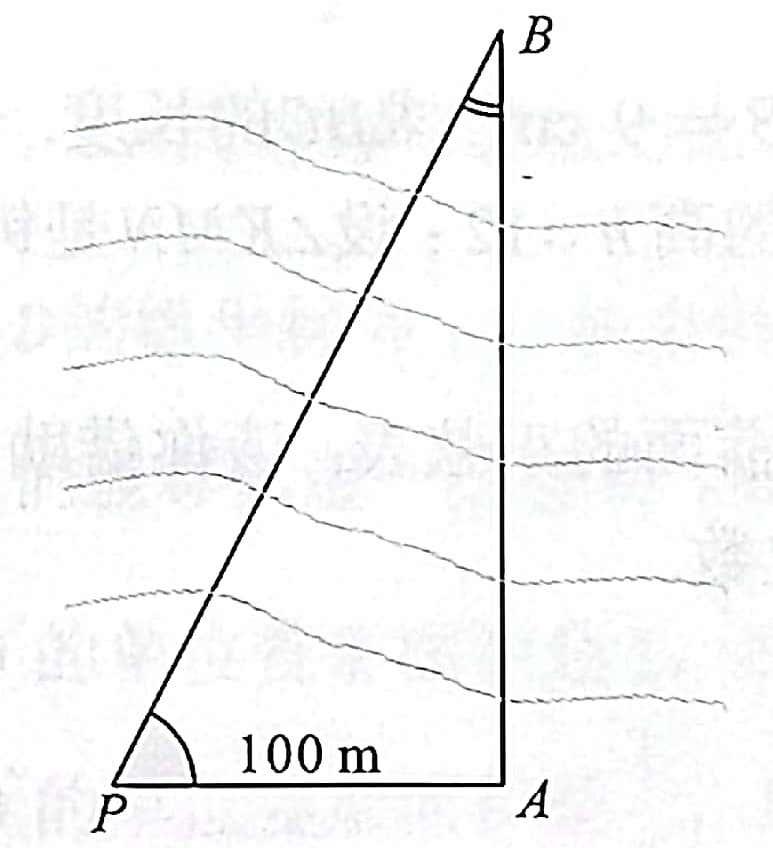
练习:(三角测距法)10 如图 20 所示,为了测量 \(A\) 处到河流对岸一建筑物 \(B\) 的距离,在此岸边另选一点 \(P\) ,使得 \(PA\perp AB\) ,\(PA=100m\)。测得 \(\angle{P}=62^\circ\) 。计算 \(A\) 到 \(B\) 的距离。
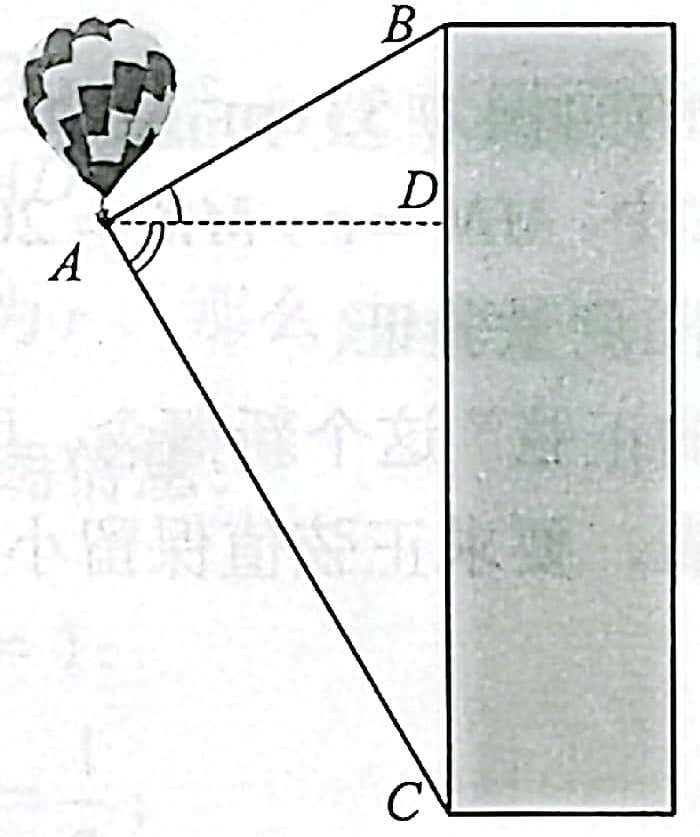
练习:(三角测距法 A)11 如图 21 所示,热气球探测器显示,从热气球看一栋楼顶部的仰角为 \(30^\circ\) ,看这栋楼底部的俯角为 \(60^\circ\) ,热气球与楼的水平距离为 \(120m\) ,这栋楼有多高?(结果取整数,单位为 \(m\))
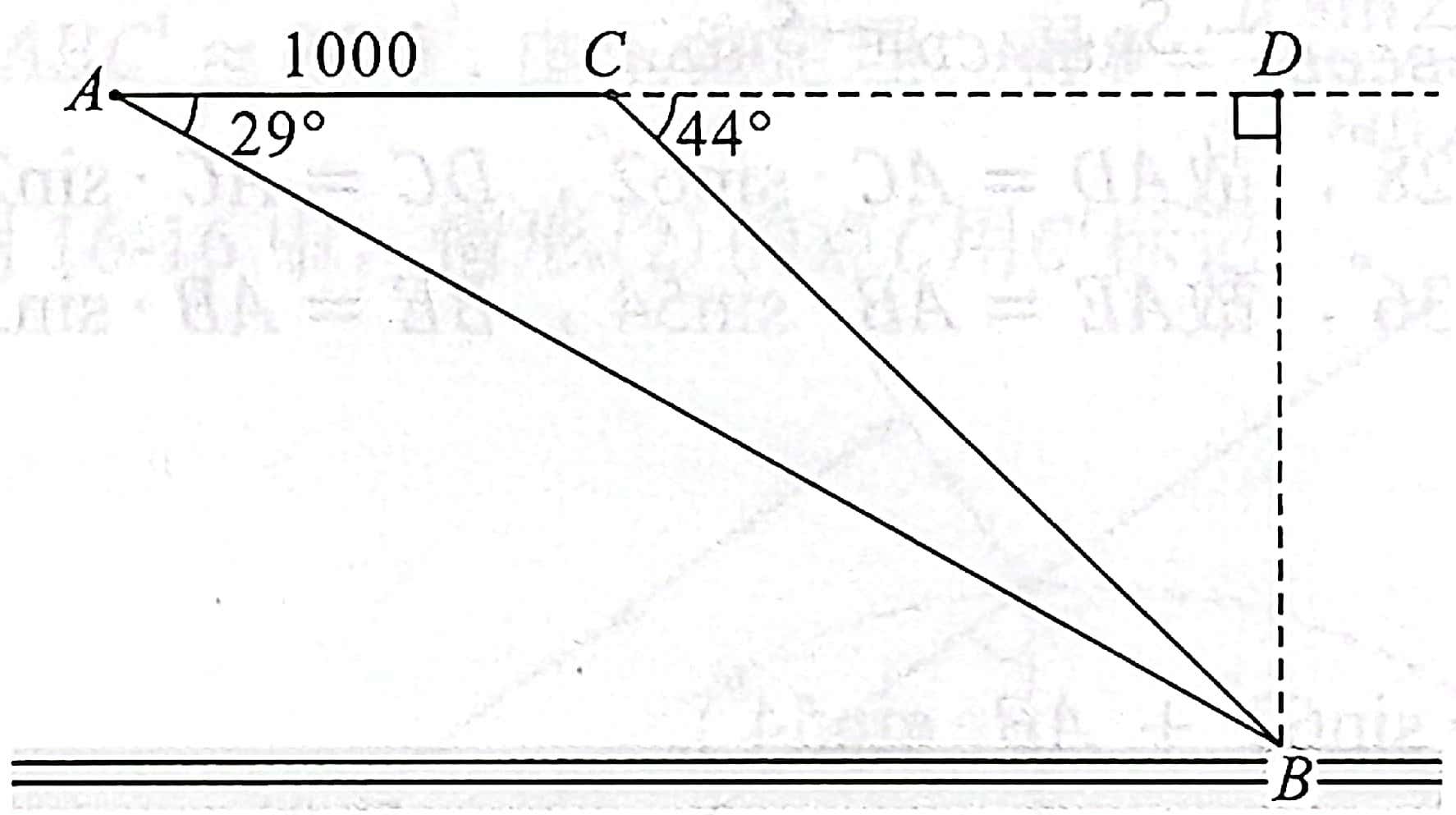
练习: 如图 22 所示,12 直升飞机于空中 \(A\) 处观测正前方地面上一目标 \(B\) 的俯角为 \(29^\circ\) ,继续向前飞 \(1000\) 米到 \(C\) 处,观测到目标 \(B\) 的俯角为 \(44^\circ\) 。问飞机向前再飞行多远,才能到目标 \(C\) 的正上方?飞机到地面的高度是多少?
本题要使用三角函数表
本题要使用三角函数表
在现阶段,只要求采用三角函数表求解近似值。在学习过和角的三角函数之后,我们可以精确求出此处的三角函数值
基础练习:正弦定理
练习: (三角测距法 B)16 为测量 \(A\) 处到河对岸 \(B\) 处的距离,在河岸 \(A\) 所处一侧选取一点 \(P\) ,使得 \(PA=200m\) 。测得 \(\angle{P}=62^\circ\) ,\(\angle{A}=43^\circ\) 。
画出\(A,B,P\) 以及河流位置的示意图;
试计算 \(A,B\) 两点之间的距离。
练习:17 在 \(\triangle{ABC}\) 中,已知 \(\angle{A}=35^\circ\) ,\(a=6\),\(c=9\) ,求 \(\angle{B}\) 和 \(b\) 。(结果角度准确到 \(0.5^\circ\) ,长度保留两位小数)
练习:18 在 \(\triangle{ABC}\) 中,已知 \(\angle{A}=35^\circ\) ,\(a=6\),\(c=4\) ,求 \(\angle{B}\) 和 \(b\) 。(结果角度准确到 \(0.5^\circ\) ,长度保留两位小数)
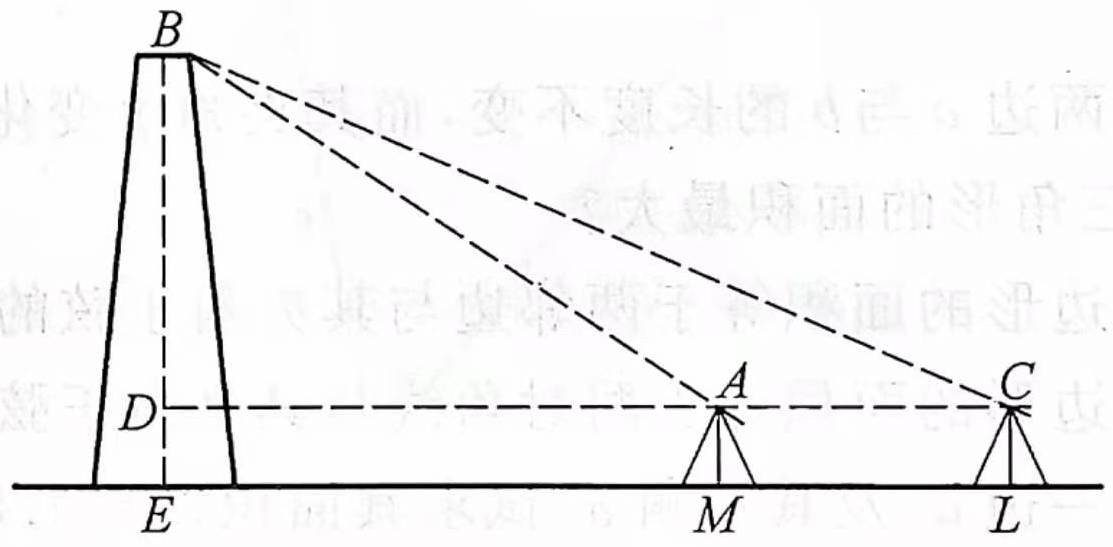
练习:19 如图 24 所示,欲测不能到达其底部的工厂之烟囱高度,若已测量指向烟囱底部之基线 \(AC=11m\) ,且 \(\angle{BAD}=49^\circ\) ,\(\angle{BCD}=35^\circ\) ,及量角器之高 \(AM=1.37m\) ,问烟囱的高度如何?
练习:20 为了测量铅直物体 \(AB\) 的高,由底端引一基线 \(AC\) 与地面成 \(\alpha\) 角,由点 \(C\) 仰望点 \(B\) ,其仰角为 \(\beta\) , \(AC=b\mathrm{m}\),求此物体的高。21
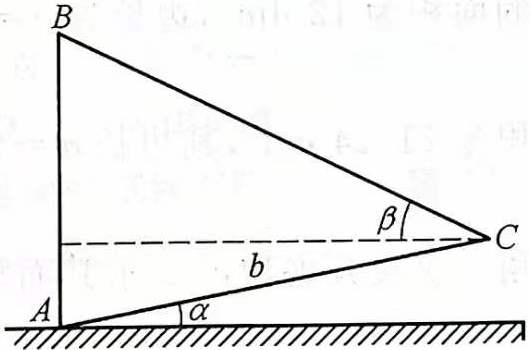
练习:22 在与地面成 \(\beta\) 角的山坡上耸立一树,当太阳高度角为 \(\alpha\) 时,树在坡上的影子长为 \(l\mathrm{m}\) ,求树高。
练习:23 平行四边形的一对角线长为 \(d\) ,且此对角线将平行四边形的二对角分为 \(\alpha\) 及 \(\beta\) ,求此平行四边形的各边长度。
练习:24 已知三角形的二角\(\beta\) 与 \(\alpha\) ,及其夹边 \(a\) ,求该三角形各内角平分线的长度。
练习:25 在 \(\triangle{ABC}\) 内,已知 \(\angle{A}=\alpha\) ,\(\angle{C}=\gamma\) ,高 \(AD=h\mathrm{m}\),求三角形各边之长。
基础练习:余弦定理
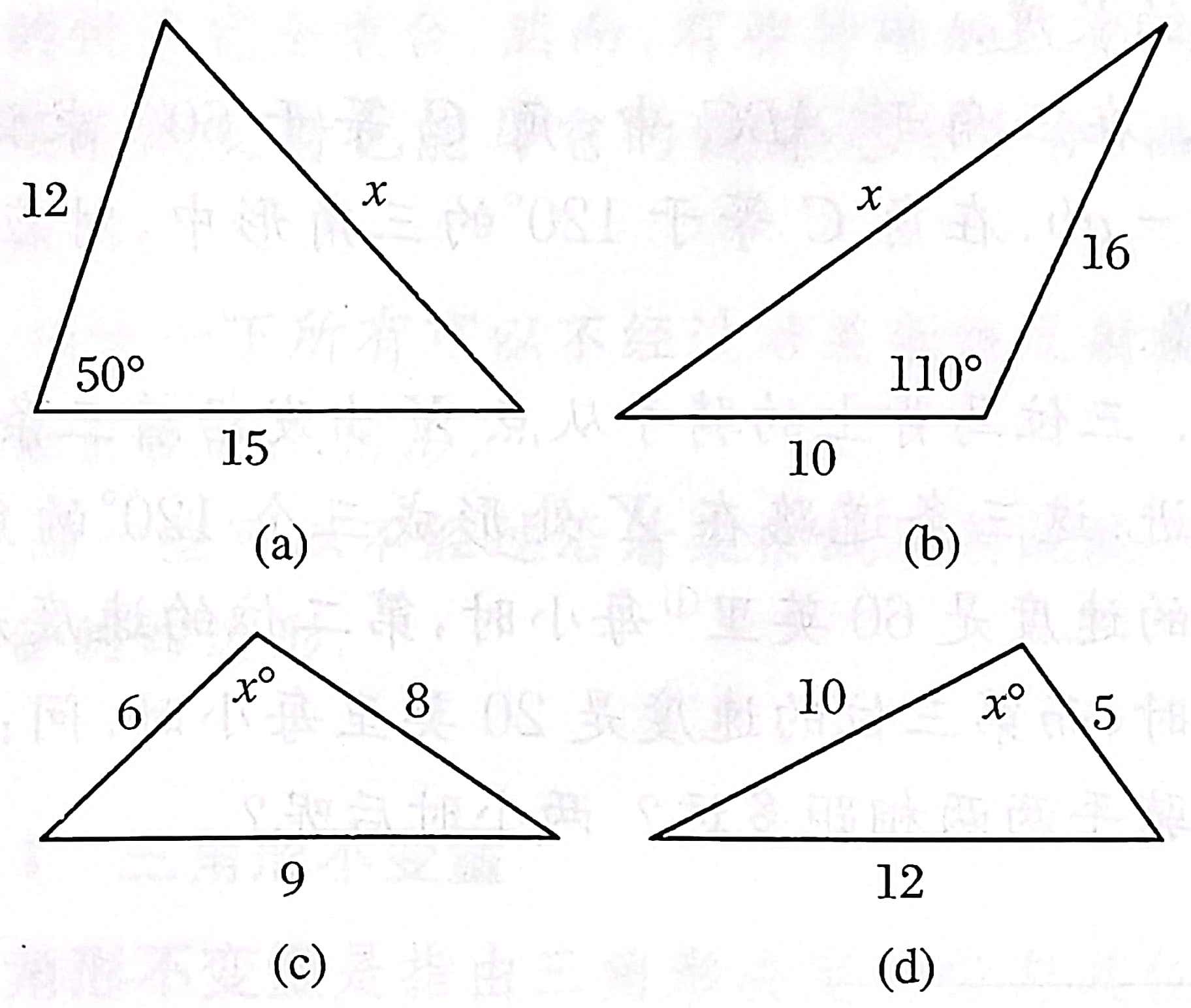
练习:26 对于下图中的每个三角形,求标有 \(x\) 的边或者角。
练习:28 由下列已知条件,解三角形:
\(a=10,b=15,\angle{C}=123^\circ17'\)
\(a=0.2,c=0.6,\angle{B}=23^\circ28'\)
\(c=40,a=100,\angle{C}=16^\circ28'\)
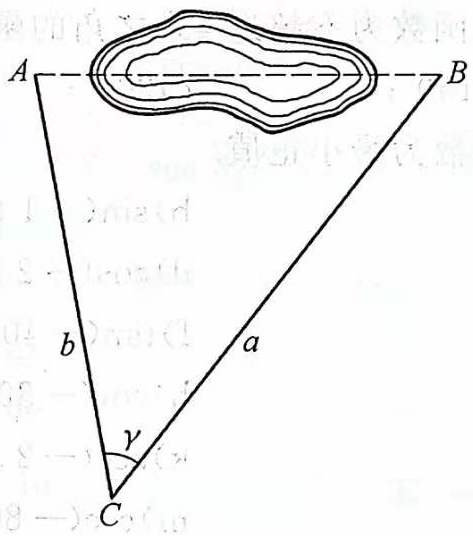
练习:29 欲测不能直接测得之两地 \(AB\) 间的距离,如图 27 所示。通过能直接看到 \(A,B\) 两地之一地 \(C\) ,并测得距离 \(BC=a\) ,\(AC=b\) 及 \(\angle{ACB}=\gamma\) ,试求 \(A,B\) 间的距离。\ (\(a=100\mathrm{m},b=80\mathrm{m},\gamma=48^\circ57'\))
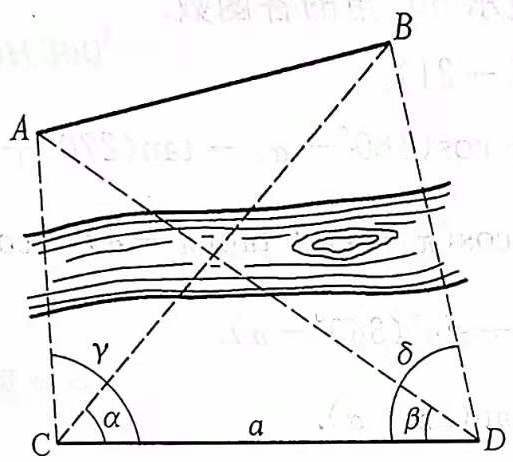
练习:32 如图 28 所示,已知不过 \(A,B\) 两地的基线 \(CD=a\mathrm{m}\) ,\(\angle{ACD}=\gamma\) , \(\angle{BCD}=\alpha\) , \(\angle{BDC}=\delta\) , 求 \(AB\) 。\ (\(a=2000\mathrm{m},\alpha=52^\circ40',\beta=42^\circ1',\gamma=86^\circ40',\delta=81^\circ15'\))
基础练习:面积公式
练习:33 求证平行四边形的面积等于两邻边与其夹角正弦的乘积。补充练习:三角函数的概念
练习:39 若扇形 \(OAB\) 的圆心角是 \(\theta\) ,半径是 \(a\)
试用 \(a\) 和 \(\theta\) 表示这个扇形内切圆的半径 \(r\) 。
若扇形的圆心角是 \(60^\circ\) ,求其内切圆与扇形的面积之比。
练习:40 求弦长是 \(a\) ,且包含 \(60^\circ\) 圆周角的弓形面积。
练习:41 若正多边形的一个外角是一个内角的 \(\dfrac{1}{6}\) ,试用弧度制表示内角和外角的大小,并求出多边形的边数。
练习:42 将下列各角换算成弧度制或角度制
\(75^\circ,\ 120^\circ,\ -150^\circ,\ -300^\circ,\ 175^\circ,\ -36^\circ\)
\(\dfrac{\pi}{10},\ \dfrac{5\pi}{2},\ -\dfrac{3\pi}{4},\ \dfrac{2\pi}{3},\ 2,\ -3\)
练习:43 两个相等的圆 \(O,O'\) 相交于 \(A,B\) 两点,它们公共部分的面积等于圆 \(O\) 面积的一半。令 \(\angle{AOB}=\dfrac{\pi}{2}+\theta\) 。求证 \(\theta=\cos\theta\)
练习:44 用作图的方法求出 \(\sin15^\circ\) 和 \(\cos15^\circ\) 的值。
练习:45 用作图的方法求出 \(\sin18^\circ\) 和 \(\cos18^\circ\) 的值。
练习:46 证明下列等式:
\(\tan^2 x+(1-\tan^4 x)\cos^2 x=1\)
\(\dfrac{\sin(90^\circ-x)}{\tan(90^\circ-x)}=\sin x\)
\(\dfrac{1}{1+\sin x}=\dfrac{1}{\cos^2 x}-\dfrac{\tan x}{\cos x}\)
练习:47 证明下列等式:
\(\dfrac{1+2\sin\theta\cos\theta}{\cos^2\theta-\sin^2\theta}=\dfrac{\cos\theta+\sin\theta}{\cos\theta-\sin\theta}\)
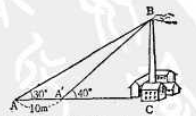
练习:48 要测量烟囱的高度,但由于它的周围有建筑物而不能测得到烟囱底部的距离。现在空地上取 \(A,A'\) 两点,使 \(A,A',C\) 在一条直线上。分别在 \(A,A'\) 测仰角,得 \(\angle{A}=30^\circ\) ,\(\angle{A'}=40^\circ\) ,又测得 \(AA'=10m\) 。求烟囱的高度。
练习:49 求下列三角形的面积:

练习:50 若菱形的边长是 \(20\mathrm{cm}\) ,一个角是 \(60^\circ\) ,求它的内接正方形的边长。
练习:51 梯形的上底是 \(a\) ,下底是 \(b\) ,\(a<b\) ,两底角是 \(\alpha,\beta\) ,写出它的面积公式。
练习:52 有一个长方形的台球台 \(ABCD\) 。假设一个球从中心 \(O\) 打出后,经 \(AB\) 上的点 \(X\) 反弹到 \(BC\) 上的点 \(Y\) 。 \(AB=2a,\ BC=2b,\ \angle{AXO}=\angle{BXY}=\theta\) 。
绘制示意图;
用 \(a,b,\theta\) 表示 \(BY\) 的长;
若 \(a=\sqrt{3}b\) ,求是从 \(X\) 弹回的球恰巧进入 \(C\) 点的 \(\theta\) 的值。
练习:53 从直角三角形的顶点 \(A\) 向斜边 \(BC\) 作垂线 \(AD\) ,再从它的垂足 \(D\) 向 \(AB\) 、 \(AC\) 分别作垂线 \(DE\) 、 \(DF\) ,设 \(BC=a,\ BE=x,\ CF=y,\ \angle{ABC}=\theta\)
用 \(a\) 及 \(\theta\) 的三角函数表示 \(AB\) ;
用 \(a\) 及 \(\theta\) 的三角函数分别表示 \(x,y\) ;
证明 \(x^{\frac{2}{3}}+y^{\frac{2}{3}}=a^{\frac{2}{3}}\) 。
练习:54 \(A\) 是锐角,\(\sin A=\dfrac{1}{3}\) ,求 \(\tan A\) 及 \(\sec A\) 。
练习:55 \(A\) 是锐角,\(\cos A=\dfrac{12}{13}\) ,求 \(A\) 其它的三角函数值。
练习:56 \(A\) 是锐角,用 \(\cos A\) 表示 \(A\) 的其它三角函数值。
练习:57 \(A\) 是锐角, \(\cos A=\dfrac{7}{25}\) ,那么 \(\sin A\) 等于多少?
练习:58 \(A\) 是锐角,若 \(\cos A=\dfrac{1}{a}\) ,求 \(\sin A\) 及 \(\tan A\) 。
练习:59 \(A\) 是锐角,若 \(\cos A=\dfrac{5}{13}\) ,求 \(\sin A\) 及 \(\tan A\) 。
练习:60 \(A\) 是锐角,若 \(\tan A=\sqrt{3}\) ,求 \(\sin A\) 及 \(\cos A\) 。
练习:61 \(A\) 是锐角,若 \(\tan A=\dfrac{m}{n}\) ,求 \(\sin A\) 及 \(\cos A\) 。
练习:62 \(A\) 是锐角,用 \(\sin A\) 表示 \(A\) 的其它三角函数值。
练习:63 \(A\) 是锐角,若 \(\tan A=\dfrac{2mn}{m^2-n^2}\) 求 \(\cos A\) 及 \(\csc A\) 。
练习:64 \(A\) 是锐角,若 \(\cos A=0.7\) ,计算 \(\tan A\) ,精确到小数点后第二位。
练习:65 \(A\) 是锐角,当 \(\tan A=\dfrac{2x(x+1)}{2x+1}\) 时, \(\sin A\) 和 \(\cos A\) 的值是多少?
补充练习:三角函数的等式变形
练习:66 若 \(\sin\theta+\sin^2\theta=1\) ,求 \(\cos^2\theta+\cos^4\theta\) 的值。
练习:67 若 \(1+\sin^2\theta=3\sin\theta\cos\theta\) ,求 \(\tan\theta\) 的值。
练习:68 若 \(\cos x=\tan x\) ,求 \(\sin x\) 的值。
练习:69 若 \(\sin x+\cos x=a\) ,求 \(\tan x+\cot x\) 的值。
练习:70 化简 \((\csc\theta-\sin\theta)\cdot(\sec\theta-\cos\theta)\cdot(\tan\theta+\cot\theta)\)
练习:71 化简 \(\dfrac{\tan\theta}{1-\cot\theta}+\dfrac{\cot\theta}{1-\tan\theta}-\sec\theta\csc\theta\)
练习:72 化简 \(\cot^2\theta\cdot\dfrac{\sec\theta-1}{1+\sin\theta}+\sec^2\theta\cdot\dfrac{\sin\theta-1}{1+\sec\theta}\)
练习:73 化简 \((\sin\theta+\cos\theta)^2+(\sin\theta-\cos\theta)^2\)
练习:74 化简 \((1-\tan^4\theta)\cos^2\theta+\tan^2\theta\)
练习:75 化简 \((\tan\theta+\cot\theta)^2-(\tan\theta-\cot\theta)^2\)
练习:76 当 \(\cos\alpha=\dfrac{m^2+2mn}{m^2+2mn+2n^2}\) 时, \(\tan\alpha\) 等于多少?
练习:77 若 \(\tan\dfrac{x}{2}=t\) ,用 \(t\) 表示 \(\cos x\) 、 \(\sin x\) 和 \(\tan x\) 。
练习:78 已知 \(\sin\alpha+\sin\beta=1,\ \cos\alpha+\cos\beta=0\) ,求下列两式的值。
\(\cos2\alpha+\cos2\beta\) ;
\(\sin^4\alpha+\cos^4\beta\) 。
练习:79 证明 \(\dfrac{\sin\alpha+\cos\alpha}{\sec\alpha+\csc\alpha}=\sin\alpha\cos\alpha\)
练习:80 证明 \(\dfrac{\cot\alpha+\tan\beta}{\tan\alpha+\cot\beta}=\cot\alpha\tan\beta\)
练习:81 证明 \(\dfrac{\tan A+\tan B}{\cot A+\cot B}=\tan A\tan B\)
练习:82 证明 \(\dfrac{(\sec A+\csc A)^2}{\sec^2A+\csc^2A}=1+2\sin A\cos A\)
练习:83 证明 \((1-\tan^4A)\cos^2A+\tan^2A=1\)
练习:84 证明 \((\cos A-\cos^3A)^2+(\sin A-\sin^3A)^2=\sin^2A\cos^2A\)
练习:85 证明 \((\cos^2A+\cot^2A)\tan^2A=\sec^2A+(\cos^2A-1)\tan^2A\)
练习:86 证明 \(\sin A(1+\tan A)+\cos A(1+\cot A)=\csc A + \sec A\)
练习:87 证明 \((\tan\alpha-\sin\alpha)^2+(1-\cos\alpha)^2=(\sec\alpha-1)^2\)
练习:88 证明 \((\tan\alpha-1)^2+(1-\cot\alpha)^2=(\sec\alpha-\csc\alpha)^2\)
练习:89 证明 \(\sin^2\cos^2\beta-\sin^2\beta\cos^2\alpha=\sin^2\alpha-\sin^2\beta\)
练习:90 证明 \(\sec^2\alpha+\csc^2\alpha=\sec^2\alpha\cdot\csc^2\alpha\)
练习:91 证明 \(\tan^2\alpha+\cot\alpha+2=\sec^2\alpha\csc^2\alpha\)
练习:92 证明 \(\dfrac{2\sin\theta\cos\theta-\cos\theta}{1-\sin\theta+\sin^2\theta-\cos^2\theta}=\cot\theta\)
练习:93 证明 \(\sec^6A=1+\tan^6A+3\tan^2A\sec^2A\)
练习:94 证明 \(\dfrac{\tan A}{1-\cot A}+\dfrac{\cot A}{1-\tan A}=\sec A\csc A+1\)
练习:95 证明 \(1-\tan^2A+\tan^4A=\cos^2A(1+\tan^6A)\)
练习:96 证明 \(\tan\theta+\cot\theta=2\sin\theta\cos\theta+\sin^3\theta\sec\theta+\cos^3\theta\csc\theta\)
练习:97 若 \(m\sin\alpha=n\cos\alpha\) ,证明 \(\sin\alpha=\dfrac{n}{\sqrt{m^2+n^2}}\)
练习:98 若 \(\cos\theta=\dfrac{5}{13}\) ,计算 \(\dfrac{2\sin\theta-3\cos\theta}{4\sin\theta-9\cos\theta}\) 的值。
练习:99 若关于 \(x\) 的二次方程 \(x^2-(\tan\alpha+\cot\alpha)x+1=0\) 的一个根是 \(2+\sqrt{3}\) 。证明 \(\sin\alpha\cos\alpha=\dfrac{1}{4}\)
练习:100 证明下列等式:
\(\dfrac{1-\tan^2x}{1+\tan^2x}=\cos^2x-\sin^2x\)
\(\dfrac{\sin x}{1+\cos x}=\dfrac{1-\cos x}{\sin x}\)
\(2+\cot^2x=\dfrac{1}{\sin^2x}+\dfrac{1}{\cos^2x}-\tan^2x\)
练习:101 若 \(\cos A=\cos x\sin C,\ \cos B=\sin x\sin C\) ,证明 \(\sin^2A+\sin^2B+\sin^2C=2\)
练习:102 若 \(1+\sin^2\theta=3\cos\theta\sin\theta\) ,求 \(\tan\theta\) 的值。
练习:103 已知关于 \(x\) 的二次方程 \(3x^2-4x\sin\alpha+2(1-\cos\alpha)=0\) 有两个不相同的实根,求实数 \(\alpha\) 的取值范围。(注:原书答案需要加入锐角限定)