计数原理(一)
在 1871 年到 1884 年间,格奥尔格·康托尔 (Georg Cantor) 创建了集合论。集合论对数学研究和教学产生了深远的影响。通过对集合及其相互关系的学习,我们可以对整数的概念和运算有更深入的理解。集合的符号和语言在数学的各个领域中有着普遍的应用。
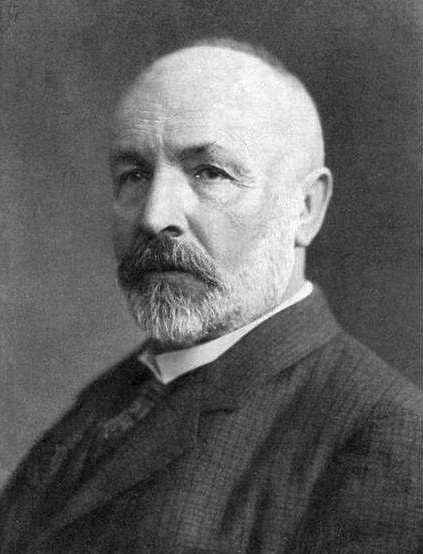
集合
集合
定义: 一般来讲,集合是具有某种特性的事物的整体,或是一些确认对象的汇集。集合中元素的次序是不重要的, \(\{a,b,c\}\) 和 \(\{c,b,a\}\) 是同样的集合。集合中没有重复的元素。
构成集合的事物或对象称作元素或是成员。集合的元素可以是任何事物,可以是人,可以是物,也可以是字母或数字等。我们常常用大写字母表示集合,将集合的元素写在花括号 \({}\) 里。例如可以使用以下标记来表示包含 \(26\) 个小写字母的集合 \(A\) 。 \[A=\{a,b,c,d,e,f,g,h,i,j,k,l,m,n,o,p,q,r,s,t,u,v,w,x,y,z\}\]
元素和集合的关系
我们使用 \(\in\) 表示某个元素属于给定集合,例如 \(b\in A\) 。如果某个元素不属于给定集合,则使用 \(\notin\) 记号,例如 \(5\notin A\) 。
\(0\) 算不算自然数
在全球范围内,目前针对 \(0\) 是否属于自然数的争论依旧存在。在中国大陆,2000年左右之前的中小学教材一般不将 \(0\) 列入自然数之内。在2000年左右之后的新版中小学教材中,普遍将 \(0\) 列入自然数。国际标准ISO 31-11:1992《量和单位 第十一部分:物理科学和技术中使用的数学标志与符号》(已被ISO/IEC 80000-2取代)中,从集合论角度规定:自然数集是包括正整数和 \(0\) 。中国大陆于 1993 年制定的强制性国家标准《物理科学和技术中使用的数学符号》(GB 3102.11-93)也参照了国际标准ISO 31-11规定。
\(N\) 在习惯上代表自然数集合。
请注意在上述描述法的表述中,逗号表示“并且”: \[C=\{x|x\in N\quad and\quad x<10\}\]
示例: 将以下等差数列形成的集合由列举法改写成描述法:
\(\{2,4,6,8,10,...\}\)
\(\{1,3,5,7,11,...\}\)
解: a. \(\{x|x=2n+2,n\in N\}\)
- \(\{x|x=2n+1,n\in N\}\)
思考与讨论
- 上述集合描述记法和通项公式有何相同和不同之处?
集合和集合的关系
我们使用 \(\in\) 表示某个元素属于给定集合,例如 \(b\in A\) 。如果某个元素不属于给定集合,则使用 \(\notin\) 记号,例如 \(5\notin A\) 。
加法
加法原理
加法原理是一个基本的计数原理。简单描述就是:如果做某件事情有若干类方法,而每类方法各有若干种选择,那么所有的选择数目就是将各类方法的选择数量相加。
如果你在学习这一章的时候还没有学过“集合”这一概念,你可以简单跳过下面的定义。
加法原理的集合描述
设集合 \(S\) 被划分为两两不相交的部分。则 \(S\) 的对象数目可以通过确定它的每一个部分的对象数目并如此相加而得到。
你可以简单地将上述描述理解为“整体等于部分之和”。
♣ 在读到上述抽象的定义时,无法理解是很正常的一件事。你要做的就是再读一遍,并且举几个具体的例子来辅助理解。请在下面的空白出举出几个具体的例子。
加法原理的简单示例
☐
上面的例子很简单,这显然无法让我们感觉到数学的威力。接下来我们要看看这个核心原理是如何用来解决复杂问题的。加法原理的蕴含的深刻思想在于:
- 当问题无法解决时,尝试着手解决一个比较简单的问题;
- 将问题划分为较小的部分,分别求解,再把结果汇总;
接下来我们将通过一组示例展示上述数学思想的应用。
组合数的计算 - I
示例: 从 \(1\) \(2\) \(3\) \(4\) \(5\) 这 \(5\) 个数字中挑出 \(3\) 个数字,有多少种挑选方法?(次序不同算同一种方法,例如 \(1\) \(2\) \(3\) 和 \(1\) \(3\) \(2\) 是不区分的。)
分析一 你可以尝试写出所有的挑选组合,但当问题的规模变大时,你很容易重复或遗漏。(一个好主意是从小往大写)
分析二 首先我们尝试去解决一些比较简单的问题,看看我们能够得到一些什么结论。
如果题目的条件以数字的形式给出,你可以把题目的数字改的小一些,然后尝试求解。
子问题 a :从 \(1\) \(2\) 这两个数字中挑选 \(1\) 个数字,有几种方法?
子问题 b :从 \(1\) \(2\) 这两个数字中挑选 \(2\) 个数字,有几种方法?
这两个问题简单到足以一眼看出结果,答案分别是 \(2\) 种和 \(1\) 种。那我们再稍微让问题复杂一点。
子问题 c :从 \(1\) \(2\) \(3\) 中挑选 \(1\) 个数字,有几种方法?
子问题 d :从 \(1\) \(2\) \(3\) 中挑选 \(2\) 个数字,有几种方法?
这两个问题同样很简单,答案都是 \(3\) 。并且这两个问题实际上是相同的: \(3\) 选 \(2\) 就相当于从 \(3\) 个里选 \(1\) 个排除。类似地, \(4\) 选 \(3\) 和 \(4\) 选 \(1\) 的方法数也是一样的。对于 \(5\) 选 \(4\) 或 \(6\) 选 \(5\) 也有类似结论。
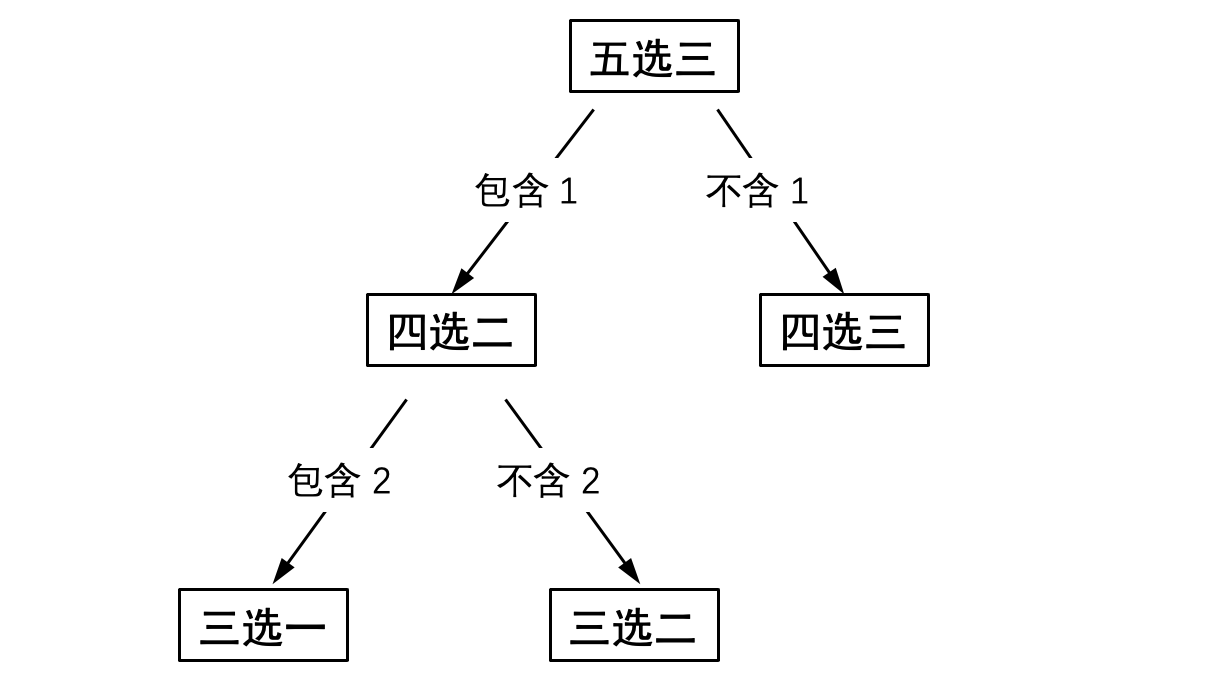
分析三 当我们处理 \(4\) 选 \(2\) 的问题时,答案就不像前几个子问题那样容易一眼看出了。这时我们进行“分情况讨论”。对于 \(1\) \(2\) \(3\) \(4\) 四个数字来说,我们可以把所有的挑选分为“包含 \(1\)”和“不包含 \(1\)”两种情况。这种划分既没有重复,也没有遗漏。如果你已经学过《逻辑与推理》一章,那你会发现“包含 \(1\)”和“不包含 \(1\)”互为命题的否定
现在我们可以正式动手来解决这个“ \(5\) 选 \(3\) ”的问题了:
解: 我们先考虑不包含 \(1\) 的情形:这相当于要在剩下的 \(2\) \(3\) \(4\) \(5\) 中再挑选 \(3\) 个。这是一个 “ \(4\) 选 \(3\) ” 问题。这很容得到对应的挑选方式为 \(4\) 种。
我们再考虑包含 \(1\) 的情形:这相当于再剩下的 \(2\) \(3\) \(4\) \(5\) 中挑选 \(2\) 个。这是一个 “ \(4\) 选 \(2\) ”问题。
从 \(n\) 个事物中选取 \(m\) 个的方法总数被称为“组合数”。在数学上用记号 \(n \choose m\) 表示组合数,有时也使用 \(C_n^m\) 表示。
上述分析过程可以写成: \[{5 \choose 3} = {4 \choose 3} + {4 \choose 2} = 4 + {4\choose2}\]
接下来我们需要看一下“ \(4\) 选 \(2\) ”问题如何处理。当然这很容易一一列举,但我们可以用类似的方法得到 \(\binom{4}{2}=\binom{3}{2}+\binom{3}{1}\) ,于是我们可以继续完成计算: \[{5 \choose 3} = {4 \choose 3} + {4 \choose 2} = {4 \choose 3} + {3 \choose 2} + {3 \choose 1}=4+3+3=10\]☐
用加法计算组合数,你需要做很多分解。毕竟是加法嘛。当我们学习乘法原理后,将给出更直接的计算方法。
上述不断将问题分解的过程如图 2 所示:
思考与讨论
- \(\binom{5}{0}\) 的值应该是多少?
- 在小学阶段课内学习中,经常遇到“五选二”的问题。回忆一下你在哪里遇到过这类问题?(参考图 3)
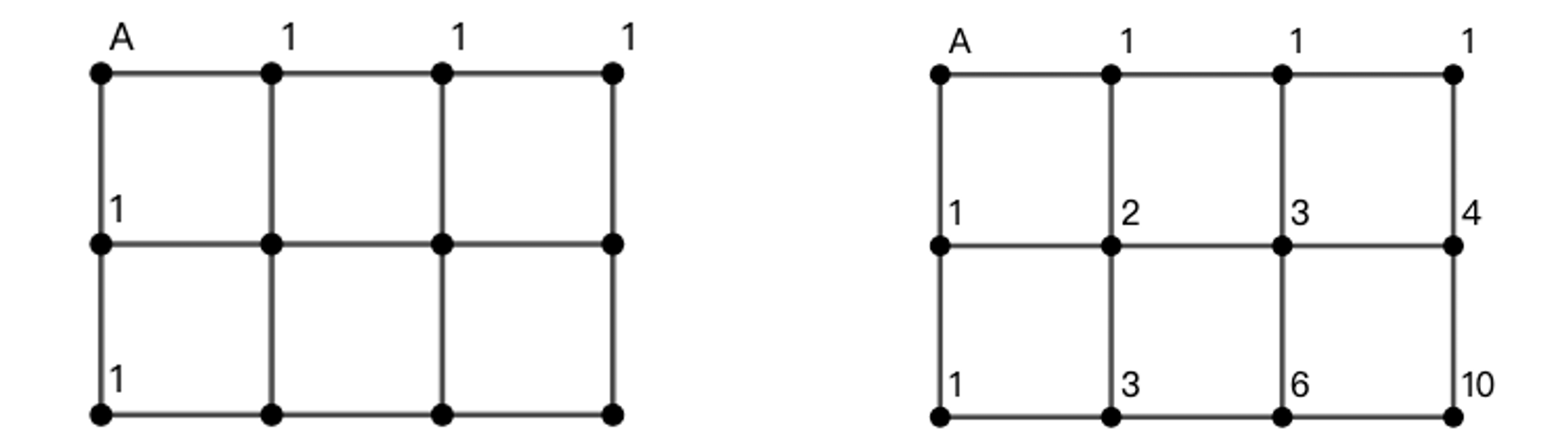
示例: 在如图 4 所示的网格道路中,我们要从 A 走到 B ,每次只能向下或向右走(不能走回头路)。总共有多少种不同的走法?
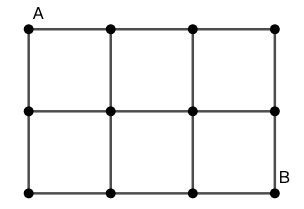
分析一 直接数肯定不是一个好主意。我们先来试图解决比较小的问题。数一数在图 5 中的网格道路中,从 A 走到 B 的路径数。
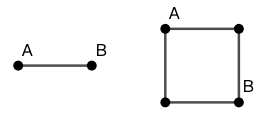
分析二 再来数一数下面的网格道路的路径数:
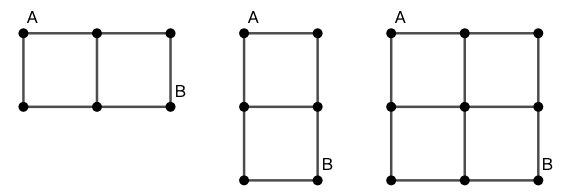
分析三 我们站在图 7 的 X 点思考一下,如果要走到 X 点,你或者需要先走到 \(1\) ,或者需要先走到 \(2\) 。所以你能走到 X 的路径数就是走到 \(1\) 和 \(2\) 的路径数之和。
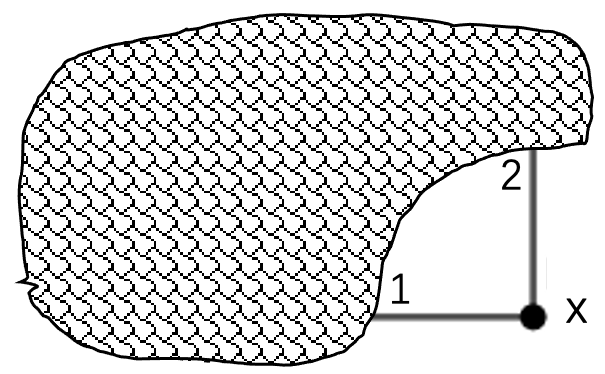
☐
思考与讨论
- 你有没发现这个例子的答案和前面那个“ \(5\) 选 \(3\) ”的例子的答案是相同的?
- 比对一下“ \(5\) 选 \(3\) ”的例子中的中间结果和本题的中间结果,你能发现什么?
- 这两个问题有着相同的答案,它们的数学结构相同么?也就是说,你能解释为什么答案相同么?
(选学)钢条切割问题
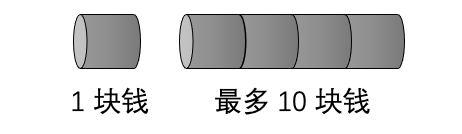
1 在本小节中,我们将用一个切割钢条的问题向你展示如何从较小问题的解得到大问题的解。让我们先来看一下问题背景: Serling 公司购买钢条切割为不同长度出售。不同长度的钢条价格如图 9 所示。假定切割工作本身没有成本支出,公司管理层希望知道最佳的切割方案。

示例: 将一段长度为 \(4\) 的钢条切割为整数长度的钢条出售(也可以不切割直接卖),总价最高的切割方式是什么?
解: 本问题中钢条的长度较短,细心地列举各种切割情况再计算总价即可。从图 10 可以看出,最佳的切割方法是将钢条切割为两条长度为 \(2\) 的短条,售价为 \(10\) 。☐
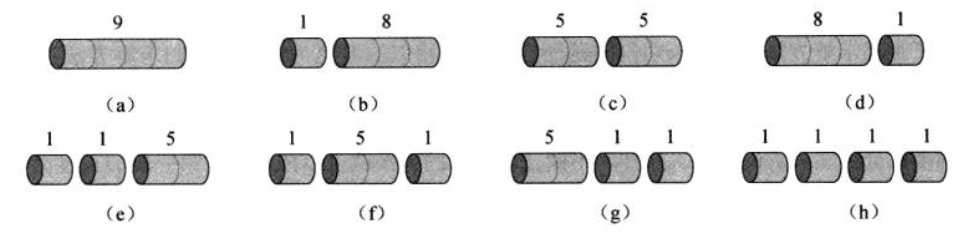
其实在图 10 列举的切割方式中,不同的切割方式只有 \(5\) 种。 \[4=1+3=2+2=1+1+2=1+1+1+1\] 你只需要计算这 \(5\) 种切割方式,从上述问题的解法指引我们讨论全部的切割方式的数目。如果我们能够枚举全部的切割方式,那么依次计算价格,就可以得到最佳切割方式。我们将在接下来的示例中讨论如何计算和枚举不同的切杆方式。
像前面的问题一样,为了方便讨论,我们引入一些记号来表示切割的数目。比如上述示例,将长度为 \(n\) 的钢条切割成不大于 \(k\) 的小段(长度均为整数)的全部方法数目记为 \(cut(n,k)\) 。上述问题的切割方法就记为 \(cut(4,4)=5\) 。进一步,我们将 \(cut(n,n)\) 记为 \(cut(n)\) 。
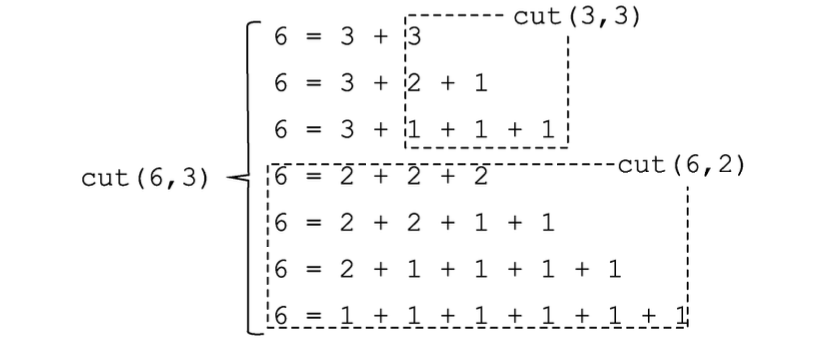
示例: 将一根长度为 \(6\) 的钢条,切割成长度(整数)不大于 \(3\) 的小段的全部方法有多少?
解: 根据前面引入的标记,本题就是要求出 \(cut(6,3)\) 的值。分两种情况讨论:(1)切出长度为 \(3\) 的小段,(2)不切出长度为 \(3\) 的小段。
在(1)中,问题转化为将剩下的长度为 \(3\) 的钢条切分为长度不大于 \(3\) 的小段即 \(cut(3,3)\) 。在(2)中,问题转化为将原有长度 \(6\) 的钢条切分为长度不大于 \(3\) 的小段即 \(cut(6,2)\) 。 \[cut(6,3)=cut(3,3)+cut(6,2)\]
于是我们将一个问题转化为两个比较简单的小问题。这样一来我们写出全部的拆分方式就容易得多,如图 11 所示:
☐
思考与讨论
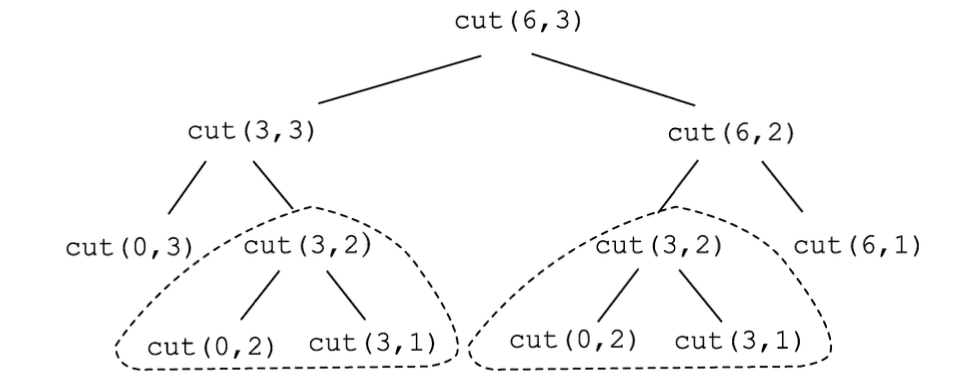
- 我们可以继续拆分问题,直至无法再分,如图 12 所示。请写出所有子问题的解,即图中所有的 \(cut(x,y)\) 的值;
- \(cut(0,2)\) 的含义是什么,它的值应当是几?
- 你观察到了多少重复计算,你实际上只需要计算几次加法?
- 画出 \(cut(7,4)\) 的子问题拆分图,统计一下需要计算几个子问题和几次加法。
示例: 这次钢条的长度为 \(8\) ,将其切割为长度不大于 \(8\) 的小段。不同长度的价格依然如图 13 所示。请问总价最高的切割方式是什么?

解: 我们从小的问题做起,然后将大问题转化为小问题进行处理。首先可以很容易得到长度为 \(1\) \(2\) \(3\) \(4\) 的最佳切割方式和价格:
- 长度为 \(1\) :\(1=1\) ,价格为 \(1\) ;
- 长度为 \(2\) :\(2=2\) ,价格为 \(5\) ;
- 长度为 \(3\) :\(3=3\) ,价格为 \(8\) ;(长度为 1 2 3 时,不切最合适)
- 长度为 \(4\) :\(4=2+2\) ,价格为 \(10\) ;(长度为 4 时已经算过了)
接下来我们看长度为 \(5\) 的钢条。我们无需列举所有的切分方式并挨个计算总价,我们只需分出五种情况:
- 第一刀切出的长度为 \(1\) ;
- 第一刀切出的长度为 \(2\) ;
- 第一刀切出的长度为 \(3\) ;
- 第一刀切出的长度为 \(4\) ;
- 第一刀切出的长度为 \(5\) ;
以第一种情况为例,在切下长度为 \(1\) 价格为 \(1\) 的小段后,问题转化为长度为 \(4\) 的最佳切割问题 \(cut(4,4)\) ,如图 14 所示。我们已经切过长度为 \(4\) 的,最佳切割为 \(4=2+2\) ,最佳价格为 \(10\) 。因此我们知道,上来先切下 \(1\) 后,最多能卖 \(1+10=11\) 元。用类似的方法可以求出五种情况的最佳价格分别为:
- 第一刀切出的长度为 \(1\) ,最佳价格为 \(1+10=11\);
- 第一刀切出的长度为 \(2\) ,最佳价格为 \(5+8=13\);
- 第一刀切出的长度为 \(3\) ,最佳价格为 \(8+5=13\);
- 第一刀切出的长度为 \(4\) ,最佳价格为 \(9+1=10\);
- 第一刀切出的长度为 \(5\) ,最佳价格为 \(10+0=10\);
第二种和第三种的价格最高,对应的切割方式为 \(2+3\) 和 \(3+2\) (实际上相同)。于是我们得到了长度为 \(5\) 的最佳切割方式和价格。
这种计算方法的好处是,你只需要做 \(5\) 次加法,就可以得到长度为 \(5\) 的钢条的最佳切割。如果你列举全部的切分方式,那么每种切分方式你都需要做好几次加法才能得到总价。当钢条的长度增加时,这种方法的优势会更加明显,因为仅仅是全部的切分方式的数量就已经数不胜数。
在考虑长度为 \(6\) 的最佳切割时,也使用类似的方法,请读者自行完成分情况讨论和计算过程:
你能依此类推,得到长度为 \(7\) 和 \(8\) 的最佳切割么?
乘法
就像乘法是加法的扩展一样,乘法原理 (Multiplication principle) 是加法原理的推论。
乘法原理
如果做一件事情有 \(n\) 个步骤,每个步骤 \(i\) 有 \(A_i\) 种方法,那么完成这件事情共有 \(A_1\times A_2\times ... \times A_n\) 种不同的方法。
用集合的语言描述乘法原理要稍微复杂一些。下面以两个集合为例描述这个原理:
乘法原理的集合描述
令 \(S\) 是对象的有序对 \((a,b)\) 的集合,其中第一个对象 \(a\) 来自大小为 \(p\) 的一个集合,而对于对象 \(a\) 的每个选择,对象 \(b\) 有 \(q\) 种选择。于是, \(S\) 的大小为 \(p\times q\) 。
乘法原理的应用
我们用一个日常生活中的常见示例来讲解乘法原理的应用:
示例: DQ 是享誉全球的冰激凌品牌。DQ 的暴风雪冰激凌有三种冰激凌基底“冰激凌原味”、“草莓芝士味”和“朗姆酒葡萄味”。你还可以添加一些小料,如图 15 所示。请问任选一种基底和任选一种辅料,一共能组合出多少种不同口味的冰激凌?

☐
乘法原理是加法原理的延续。当我们分情况讨论做某件事的方法时(不重不漏),如果各种情况的方法数一样,那么就可以用乘法直接计算。
示例: 确定 \(300\) 的正整数因子的个数。
示例: 使用 \(1\) \(2\) \(3\) 这三个数字,能组合出多少个不同的两位数?(数字可以重复)我们选用很少的数字,这样你可以很容易地通过枚举的方式验证计算结果
☐

示例: 使用 \(1\) \(2\) \(3\) 这三个数字,能组合出多少个不同的两位数?(数字不可以重复)
在解题时,你需要根据题意谨慎处理各个步骤的选择数目。
示例: 使用 \(0\) \(1\) \(2\) \(3\) 这三个数字,能组合出多少个不同的两位数?(数字可以重复)
示例: 使用 \(0\) \(1\) \(2\) \(3\) 这三个数字,能组合出多少个不同的两位数?(数字不可以重复)
排列数的计算
本节我们讨论一类常见的乘法原理问题:排列。
排列
排列是指从 \(n\) 个不同的事物中挑选 \(r\) 个事物的有序放置。
示例: 从 \(1\) \(2\) \(3\) \(4\) 中挑选两个不同的数字组成三位数,一共能组成多少个不同的三位数?
解: 组成三位数的步骤分为三步
- 第一步填入百位数,有四种选择;
- 第二步填入十位数,因为百位数已经占用了一个数字,所以还剩三种选择;
- 第三步填入个位数,有两种选择。
☐
上述问题就是从 \(4\) 个不同的事物中挑选 \(3\) 个进行有序放置。这一类问题的有序放置数目被称为“排列数”
排列数的计算公式
从 \(n\) 个不同的事物中中挑选 \(r\) 个事物的有序放置方法数量记为 \(P_n^r\) 或 \(P_n^r\) 。排列数满足如下公式: \[\begin{equation} P_n^r = n\cdot(n-1)\cdot(n-2)\cdot...\cdot(n-r+1) \end{equation}\]
也可以写作 \[\begin{equation} P_n^r = \dfrac{n!}{(n-r)!} \end{equation}\]
记号 \(n!=n\times(n-1)\times(n-2)\times ... \times1\) ,读作 \(n\) 的阶乘。
思考与讨论
- 在前一小节( 节)中的哪些问题是排列数的计算?
- 你能举出日常生活中的排列数计算问题么?
示例: 某铁路线共有 \(10\) 个客运站(含起点站和终点站),这条铁路线共需准备多少种不同的车票?

解: 根据生活经验,从 \(A\) 到 \(B\) 和从 \(B\) 到 \(A\) 是两种不同的车票。所以这是一个排列问题(\(n=10,r=2\))。
因此共有 \(P_{10}^2=90\) 种不同的车票。☐
减法
减法是加法的逆运算。在计数问题中,灵活地运用减法,反其道而行之,有时能够极大简化问题。
减法原理
有的时候为了求出某种事物的数量,我们可以求出某个包含该类事物的更大数量,再减去其余的部分。
示例: 求 \(1\) 到 \(60\) 之间不能被 \(3\) 整除的整数个数。
解: \(1\) 到 \(60\) 之间能被 \(3\) 整除的数是 \(3\) \(6\) \(9\) …. 。每三个数就有一个数能被 \(3\) 整除,所以有 \(20\) 个能被 \(3\) 整除的数。 因此, \(1\) 到 \(60\) 之间不能被 \(3\) 整除的数有 \(60-20=40\) 个。☐
示例: 某个密码锁的密码是 \(0\) \(1\) \(2\) \(3\) … \(9\) 组成的三位数字。在全部可能的密码中,有多少有重复的数字?(比如 \(001\) )
解: 直接计算带有重复数字的密码是比较令人头疼的。但我们可以容易地使用乘法原理计算出全部密码的数目为 \(9\times9\times9=729\) ,再计算出没有重复数字的密码数目为 \(9\times8\times7=504\) 。因此带有重复数字的密码共有 \(729-504=225\) 个。☐
容斥原理
当计数重复时,减去重复的部分即可。
示例: 四年级三班的小朋友都报了语文或数学课外班,报语文课外班的有 \(30\) 人,报数学课外班的有 \(25\) 人。其中有 \(10\) 位小朋友两个班都报了。请问四年级三班共多少人?
解: 如果单纯把语文班和数学班的人数相加,同时报两个课外班的小朋友就被计算了两次,如图 18 。从相加的结果里减去这些小朋友的人数就可以得到总人数。因此共有 \(30+25-10=45\) 人。☐
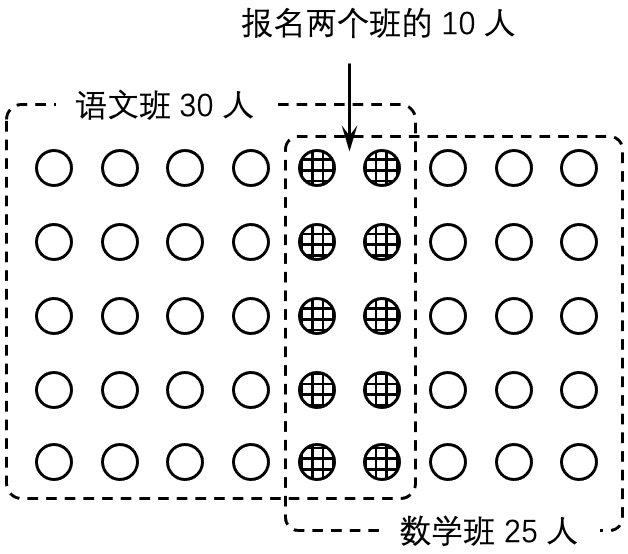
容斥原理的简单版本
“符合 A 或符合 B”的事物数量(\(A\cup B\))等于“符合 A”的事物数量(\(A\))加上“符合 B”的事物数(\(B\))量再减去“既符合 A 又符合 B”的事物数量(\(A\cap B\))。即: \[\begin{equation} A\cup B=A+B-A\cap B \end{equation}\]
当容斥原理和减法原理共同使用时,要注意“既…又…” 的反面是 “不 … 或 不 ….” ,“既不 … 又不 …” 的对立面是 “… 或 …” 。反之亦然。如图 19 所示。
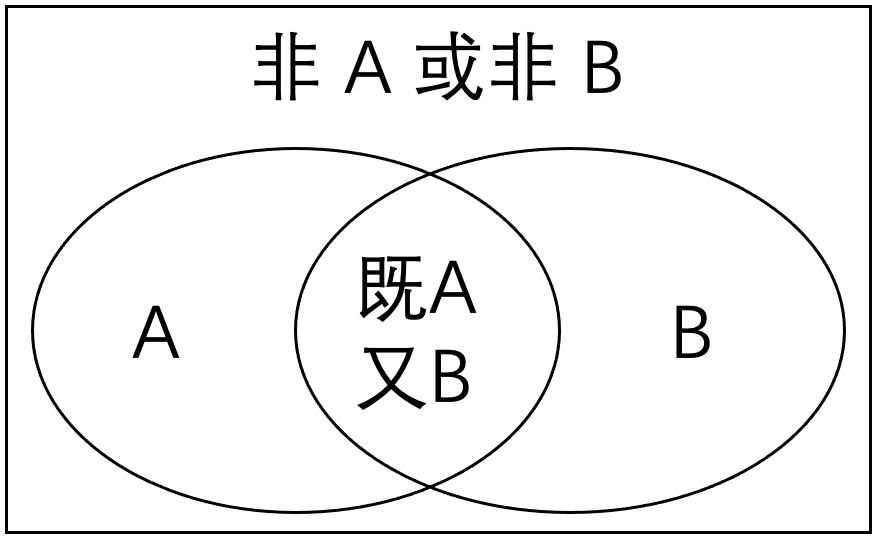
如果你已经学过《逻辑和推理》一章,你就能够知道“既…又…”和“不…或不…”互为命题的否定。如果你没学过,你也可以从日常生活经验判断。你可以试着写出几个例子来熟悉一下这些语言:
请继续看下面的例题:
示例: \(1\) 到 \(60\) 间既不能被 \(2\) 整除又不能被 \(3\) 整除的数有多少?
分析 为了计算“既不能被 \(2\) 整除又不能被 \(3\) 整除的数”的数目,只需要从全体中减去“能被 \(2\) 整除或能被 \(3\) 整除的数”的数目即可。而后者恰好符合容斥原理的模型。
解: \(1\) 到 \(60\) 之间 \(2\) 的倍数有 \(30\) 个, \(3\) 的倍数有 \(20\) 个。既是 \(2\) 的倍数又是 \(3\) 的倍数的( \(6\) 的倍数)的有 \(10\) 个。根据容斥原理, \(1\) 到 \(60\) 之间能被 \(2\) 或 \(3\) 整除的数有 \(30+20-10=40\) 个。
因此在 \(1\) 到 \(60\) 中既不能被 \(2\) 又不能被 \(3\) 整除的数总共有 \(60-40=20\) 个 。☐
示例: \(0-999\) 之间有多少个既包含 \(5\) 又包含 \(8\) 的数字?
分析 排除不包含 \(5\) 或 \(8\) 的数字即可。
解: \(0-999\) 之间的不包含的 \(5\) 的数字可以看作 \(012346789\) 数字可以重复的 \(3\) 排列,共有 \(9\times9\times9=729\) 个 。类似地可知 \(0-999\) 之间的不包含的 \(8\) 的数字也有 \(9\times9\times9=729\) 个。
\(0-999\) 之间既不包含的 \(5\) ,又不包含 \(8\) 的数字可以看作 \(01234679\) 数字可以重复的 \(3\) 排列,共有 \(8\times8\times8=512\) 个 。
所有 \(0-999\) 之间不包含 \(5\) 或 \(8\) 的数字个数为 \[9\times9\times9+9\times9\times9-8\times8\times8=946\]
综上 \(0-999\) 之间包含 \(5\) 和 \(8\) 的数字有 \(1000-946=54\) 个。☐
除法
除法将整体均匀地划分为部分。
组合数的计算 - II
如果所有的事物都被重复计算,并且重复的次数相同,就可以使用除法消除重复的次数。
重做一下 节中的组合数计算问题
分析 选 \(3\) 个数字的排列数用乘法原理很容易计算: \[P_5^3=5\times4\times3=60\] 每种选择都以 \(6\) 种不同的次序出现在这 \(60\) 种排列中,如图 20 所示。为什么是 \(6\) 呢?因为任意取 \(3\) 个数字的排列数为 \[P_3^3=3\times2\times1=6\]
解: 根据以上分析可知 \(5\) 选 \(3\) 的组合数为:\[{5 \choose 3}=\dfrac{P_5^3}{P_3^3}=10\]☐
这个结果和 节的结果是相同的。我们当然应该得到相同的结果。
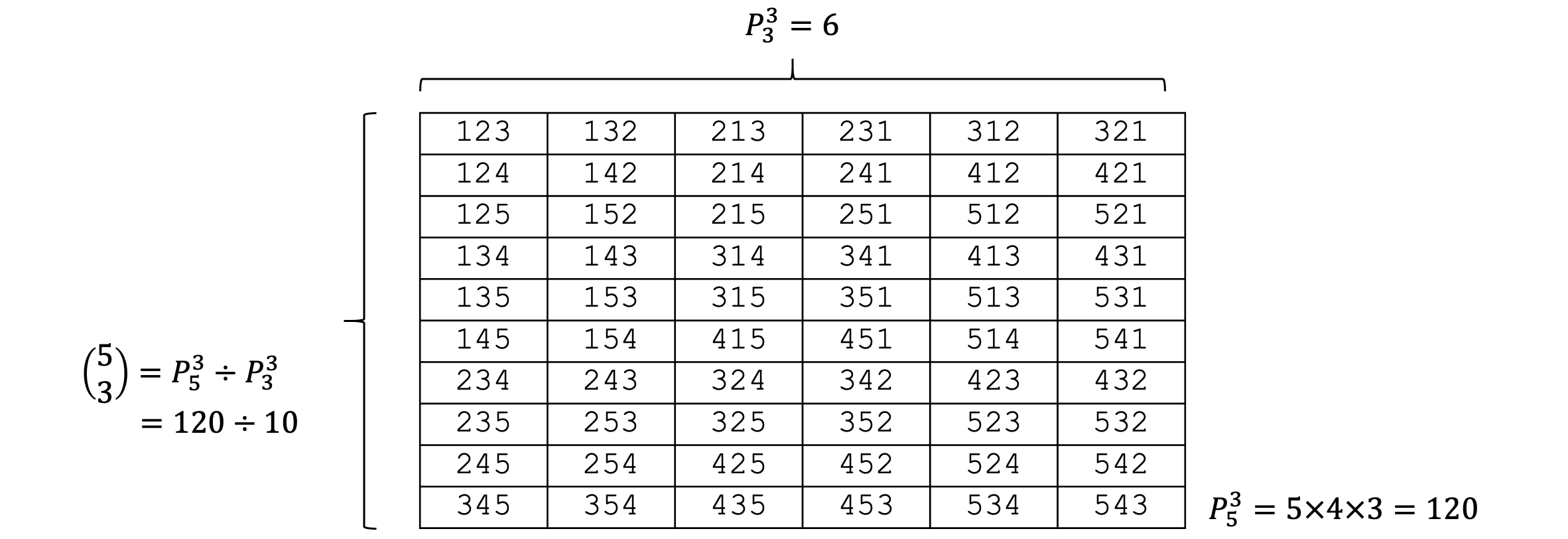
组合数的计算公式
从 \(n\) 个事物中取 \(r\) 个的组合数计算方法为: \[\begin{equation} {5 \choose 3}=\dfrac{P_n^r}{P_r^r}=\dfrac{n!}{(n-r)!\cdot r!} \end{equation}\]
鸽巢原理
本小节考虑一个重要而初等的组合学原理。这个原理叫鸽巢原理,也叫做抽屉原理。关于鸽巢原理的阐释,粗略地说就是如果有许多鸽子飞进不够多的鸽巢内,那么至少要有一个鸽巢被两个或更多的鸽子占据。下面给出更精确的叙述。
鸽巢原理的最简单形式
如果要把 \(n+1\) 个物体放进 \(n\) 个盒子,那么至少有一个盒子包含两个或更多的物体。
鸽巢原理的一个简单加强版如下所示:
鸽巢原理的常见版本一
设 \(n\) 和 \(r\) 都是正整数。如果把 \(n\cdot r+1\) 个物体分配到 \(n\) 个盒子中,那么至少有一个盒子含有 \(r+1\) 个或更多的物体。
也可以用除法描述该性质:
鸽巢原理的常见版本二
设 \(m,n,r\) 都是正整数。如果把 \(m\) 个物体放入 \(n\) 个盒子中,且 \[\dfrac{m}{n}>r\] 那么至少有一个盒子含有 \(r+1\) 个或更多的物体。
♣ 请注意,鸽巢原理对于找出含有两个或更多物体的盒子没有任何帮助,它只是保证这样的盒子存在。
示例: 在 \(13\) 个人中存在两个人,生日在同一个月份里。☐
☐
示例: 从 \(1\) 到 \(40\) 中选出 \(21\) 个整数。证明:在所选的这些整数之间存在两个整数,其中一个可被另一个整除。
随堂练习
练习: 从 \(1\) \(2\) \(3\) \(4\) \(5\) \(6\) 这 \(6\) 个数字中挑选 \(3\) 个数字,有多少种不同的方法?(不同的排列次序算相同的方法)
练习: 在 \(0\) 到 \(99\) 之间有多少个整数恰好有一位数字是 \(5\) ?
练习: 将一根长度为 \(8\) 的木杆切分为长度 \(1\) \(2\) \(3\) \(4\) 的部分,有多少种切分方法?( \(233\) 和 \(332\) 算同一种切分方法)
练习: 淘气的奶奶家在河北省的鹿泉区。淘气每年暑假回奶奶家。淘气先从北京做火车、飞机或长途汽车先到石家庄市区的叔叔家。石家庄市区到鹿泉区只有长途汽车或者出租车。请问淘气从北京到奶奶家有多少种交通工具的选择组合?
练习: 学校食堂以馒头和米饭作为主食,以宫保鸡丁、焦溜肉片和葱爆羊肉作为荤菜,还有四种素炒蔬菜,汤有鸡蛋汤和酸辣汤。请问按照一主食一荤菜一素菜一碗汤的搭配,能有多少种不同套餐?
练习: 使用 \(1\) \(2\) \(3\) 这三个数字,能组合出多少个不同的三位数?(数字可以重复)
练习: 使用 \(0\) \(1\) \(2\) \(3\) 这三个数字,能组合出多少个不同的四位数?(数字可以重复,四位数的千位不能是 \(0\) )
练习: 在所有的三位数(\(100-999\))中,有多少个数恰好有一位数字是 \(5\) ?
练习: 你有 \(100\) 个苹果、\(100\) 个橙子和 \(100\) 个梨。你至少要拿出多少个水果,才能保证至少有 \(12\) 个相同的水果?
练习: 你有 \(100\) 个苹果、\(100\) 个橙子和 \(100\) 个梨。你至少要拿出多少个水果,才能保证至少拿出 \(12\) 个苹果?
要求使用加法原理计算 \(7\choose2\) 和 \(7\choose3\)
计算组合数 \(7\choose7\), \(7\choose6\), \(7\choose5\) 和 \(7\choose4\) 。
DQ 推出暴风雪夏日优惠活动,你可以任选两份不同的辅料添加进冰激凌基底(还是 \(3\) 种基底, \(7\) 种辅料)。这回你能够组合出多少种不同口味的暴风雪冰激凌?
将一根长度为 \(10\) 的木杆切分为长度 \(1\) \(2\) \(3\) \(4\) 的部分,有多少种切分方法?(长度排列不同算同一种切法。如 \(2\) \(4\) \(4\) 和 \(4\) \(2\) \(4\) 算同一种切法。)
在图 中,从 A 出发走到 B ,只能沿线向下或向右运动。问有多少种走法?

你想送给朋友一些水果,在你面前有四个橙子,五个苹果。唯一的要求是你至少要送一个水果。请问你有多少种不同的选择?(比如你可以选择送两个橙子和一个苹果,也可以送一个橙子和一个苹果。同种的水果被认为是一样的)
用 \(1\) \(2\) \(3\) \(4\) 排列成四位数(数字不能重复),要求 \(1\) 和 \(2\) 挨在一起。请问有多少种排列方法?
要求使用加法原理进行计算
DQ 的暴风雪夏日优惠活动中,迪士尼 DQ 店为了加快制作流程,在添加辅料时,你只能在华夫脆、蜜红豆、香蕉粒和奥利奥中 \(4\) 选 \(1\) ,然后在布朗尼、芝士蛋糕和奶油中 \(3\) 选 \(1\) 。请问在这种规则下,你能够搭配出多少种不同的“迪士尼夏日暴风雪冰激凌”?
将一根长度为 \(10\) 的木杆切分为长度 \(1\) \(2\) \(3\) \(4\) 的部分,如何切卖钱最多?(长度排列不同算同一种切法。如 2 4 4 和 4 2 4 算同一种切法。)
在图 22 中,从 A 出发走到 B ,只能沿线向下或向右运动。问有多少种走法?

你想送给朋友一些水果,在你面前有四个橙子,五个苹果,六个梨。唯一的要求是你至少要送一个水果。请问你有多少种不同的选择?(比如你可以选择送两个橙子和一个苹果,也可以送一个橙子和一个梨。同种的水果被认为是一样的)
用 \(1\) \(2\) \(3\) \(4\) 排列成四位数(数字不能重复),要求 \(1\) 和 \(2\) 不挨在一起。请问有多少种排列方法?
在暴风雪夏日活动中(冰激凌基底加两份不同辅料),DQ 的店员告诉你,如果同时添加华夫脆、香蕉粒或奥利奥的口感不太好。你决定接受这个建议。请问用三种冰激凌基底和七种添加辅料,你能够作出多少种不同时含有华夫脆、香蕉粒或奥利奥的暴风雪冰激凌?
将 \(26\) 个字母排序,元音字母 aeiou 两两不能相邻,请问有多少种排序方法?
\(10\) 个小朋友玩转盘座椅游戏,每次能做 \(6\) 个人。有多少种就坐方法?(经过旋转能够相同的坐法算同一种)
从 \(10\) 种颜色的珠子中挑出 \(6\) 颗不同颜色的珠子穿成手串。有多少种不同的手串?(手串不但可以旋转,还可以翻转,旋转或翻转后相同的排列算同一种。)
魔法世界中有一片蛮荒世界,那里有着大批的探险者前去寻宝。为了更好地说明蛮荒世界,探险家在你面前展开了一幅蛮荒世界的地图。地图的左下角是部落的定居处,右上角是魔金森林,地图上方的房屋标记是探险家们在蛮荒世界中建立的据点。探险家们在蛮荒世界中探索出了一些相对安全的道路:
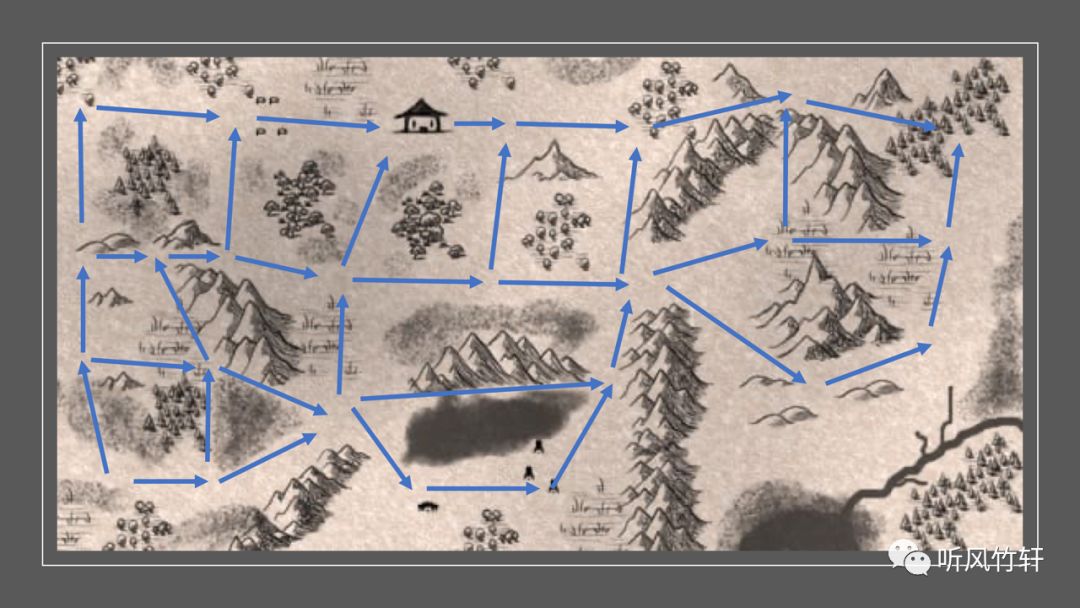
前往魔金森林的人们必须严格按照路径标记和箭头所示方向行进。即便如此,路上依然出没着各种妖兽。探险家们发现,只要每回变换去往魔金森林的道路,就能最大限度避开妖兽。探险家想让你帮他解决道路计数问题,即:在如图 23 所示的道路网络中,从一点走到另一点,有多少种不同的路径?
- [1.] 如果先走到地图的探险家据点(小房子),有多少条不同的路径?
- [2.] 如果不考虑据点(可以经过,也可以不经过)走到魔金森林,有多少条不同的路径?
十个年轻人到一家饭馆吃饭,人都到齐了,却为座位该怎么安排的问题发生了争论。有人说,应该按年龄大小来坐,也有人说,应该按个子高矮来坐。争来争去,也没有个完。这时,旁边一个老侍者说:“小伙子,你们这样争是不会有什么结果的,不如我提个建议,怎么样?”
十个年轻人不知道老侍者想说什么,于是都停住了争吵,听他开了口。老侍者说:“假如你们今天按一个排列的次序坐,明天再来吃饭时,再按着另一个次序排列,然后,后天、大后天……都按着不同的次序入座。这样,等你们十个人的次序都变换完了,再也不会有新的次序出现的时候,从那一天起,我每天免费供应你们最好的午餐,你们要什么饭菜,我给你们上什么饭菜。”
老侍者这奇怪而特别的建议引起了年轻人们的兴趣。于是,他们和老侍者约好,到了那天,一定不许反悔。年轻人们开始坐好用餐,每一个人都兴奋地想象着不用花钱吃午餐的那一天。
请你算一算,他们什么时候才能吃到免费的午餐呢?
下列各图中有多少个小于 \(180^\circ\) 的角

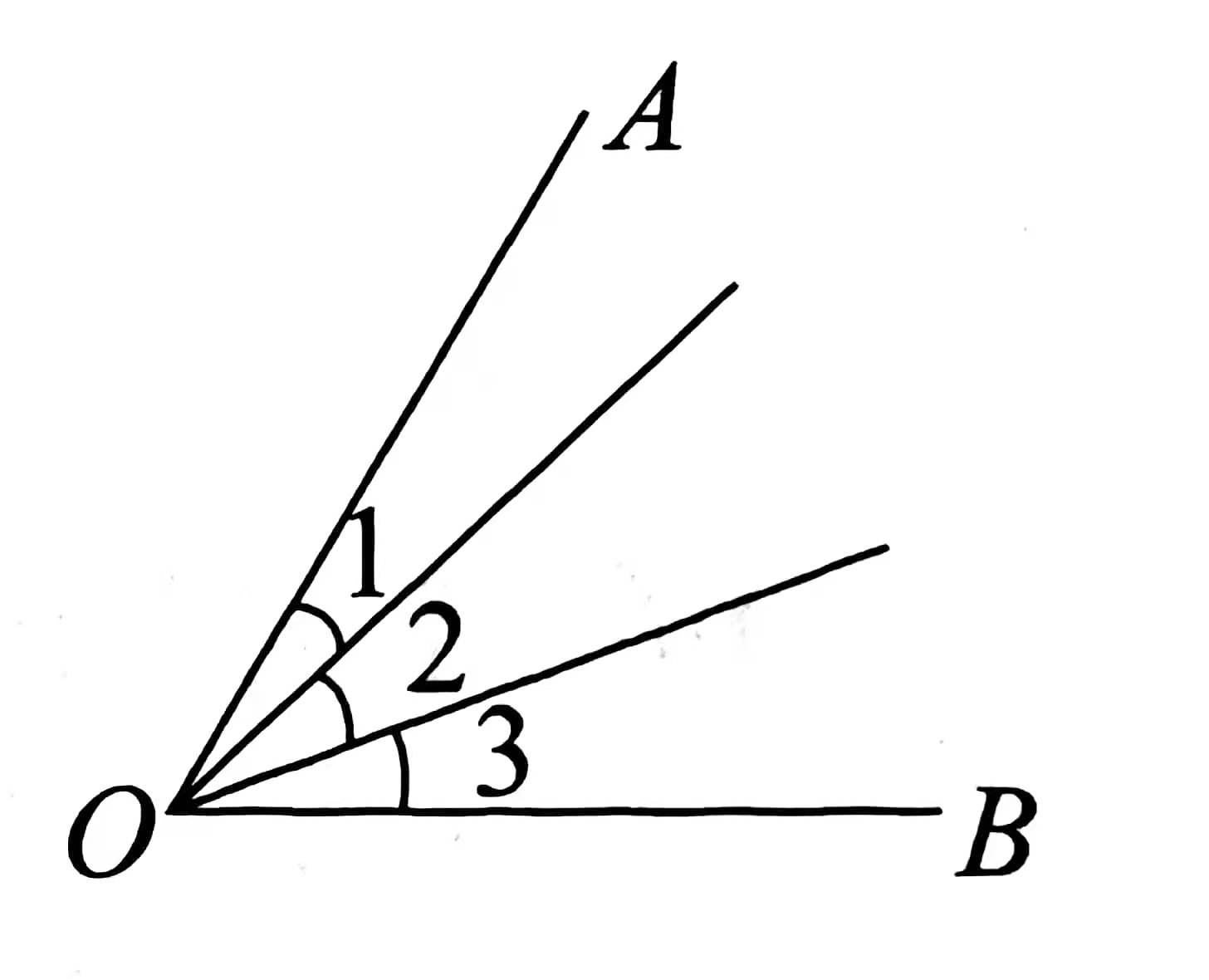
在右图中,\(\angle{1}=\angle{2}=\angle{3}\) ,如果图中所有锐角的度数之和等于 \(180^\circ\) ,那么 \(\angle{AOB}\) 是多少度?
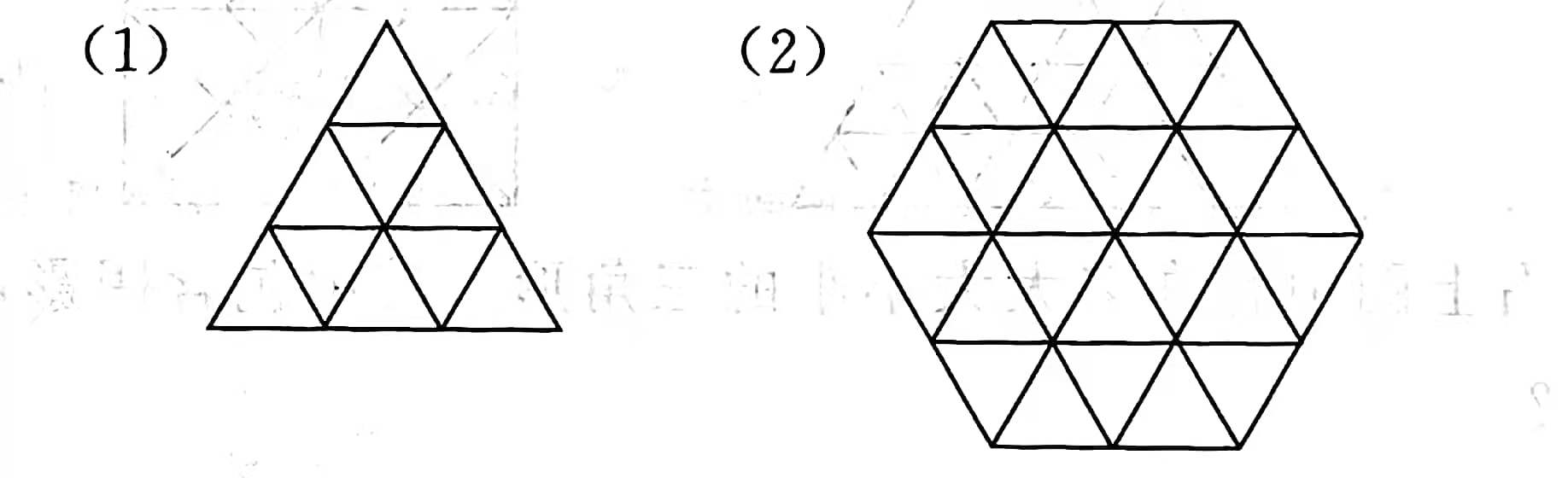
下列各图中分别有多少个三角形?

下列各图中,每个最小的正三角形的面积都等于 \(1\) ,分别求粗每个图中各种三角形的面积之和?
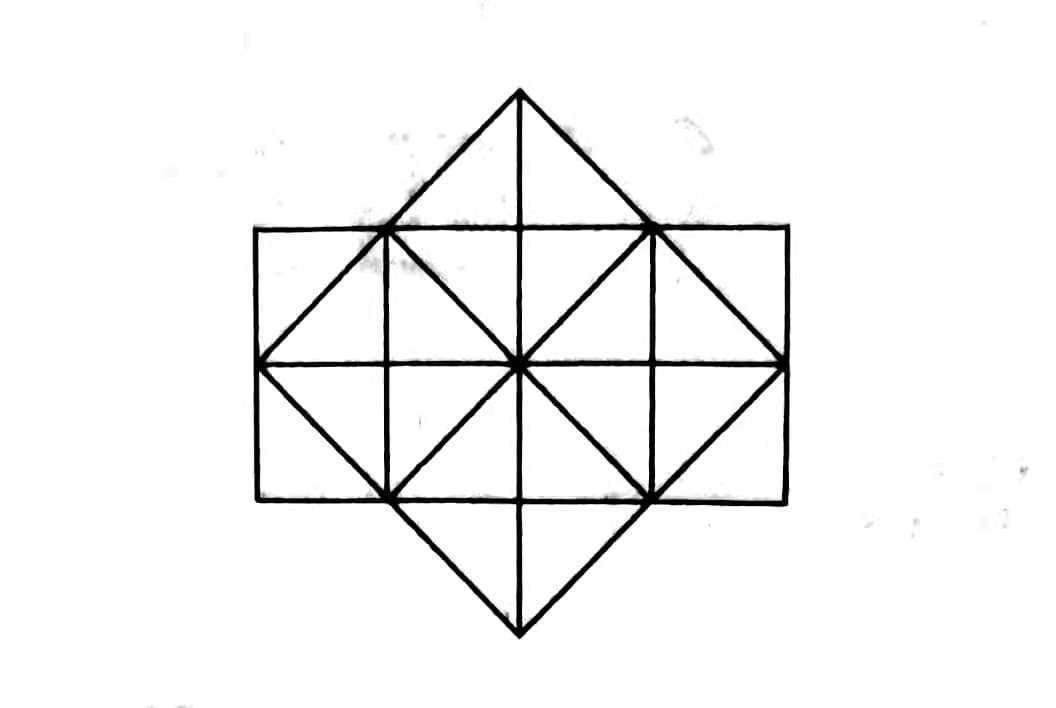
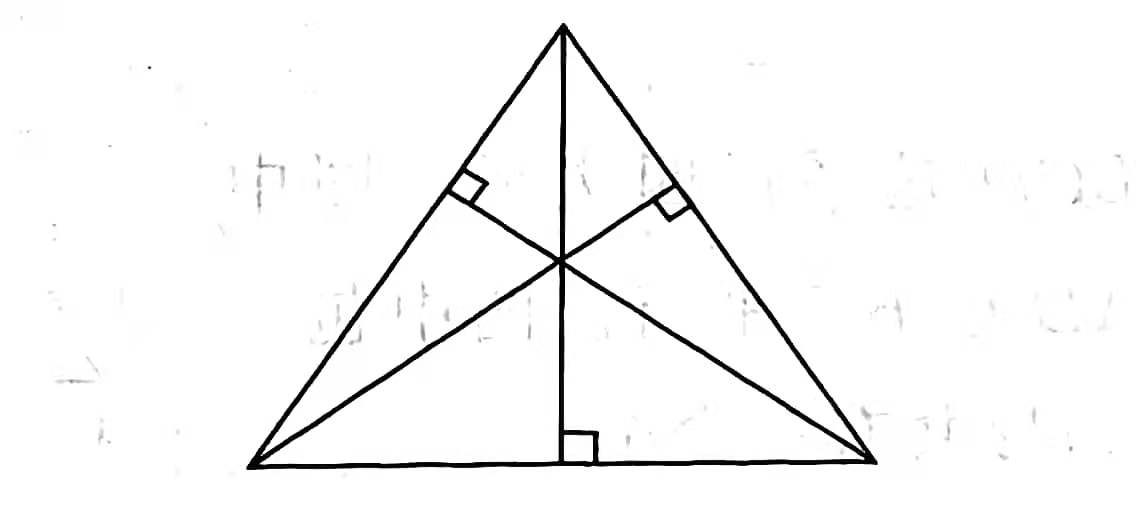
右图中共有多少个三角形?其中直角三角形有多少个?
右图中共有多少个长方形?
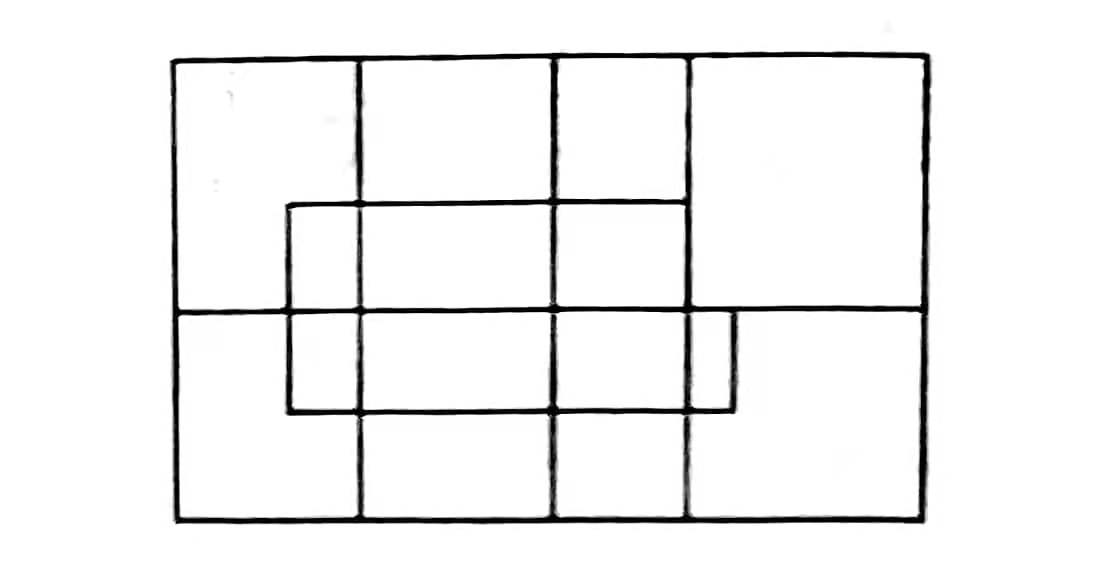
右图中共有多少个正方形?