二次函数和一元二次方程
根据给定点确定二次函数的方程
示例: 利用三元一次线性方程组确定二次函数的系数
二次函数 \(f(x)=ax^2+bx+c\) 经过点 \((-1,-3)\), \((1,3)\) 和 \((2,12)\) 。求 \(a,b,c\) 的值。
解: 将三个点的坐标代入二次函数:

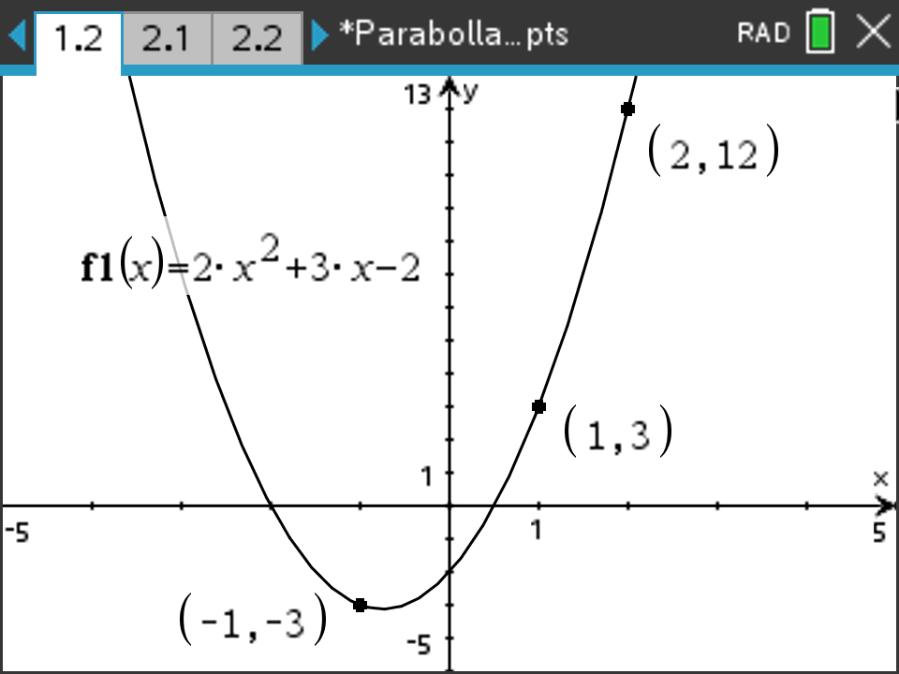
\(\begin{cases} f(-1)=-3\\ f(1)=3\\ f(2)=12\end{cases}\) 得到: \(\begin{cases} a-b+c=-3\\ a+b+c=3\\ 4a+2b+c=12\end{cases}\)
解得:\(\begin{cases} a=2\\ b=3\\ c=-2\end{cases}\)
因此二次函数为 \(f(x)=2x^2+3x-2\)☐
\(f(x)=ax+bx+c\) 和解线性方程组
\(f(x)=ax+bx+c\) 有三个系数,因此需要三个条件才能确定二次函数。解三元一次方程组进行求解是最后的底线。任何时候,你应当有信心如此求解。但在考试题目中,往往并不会直接要求你求解三元一次线性方程组。
示例: 利用截距确定 \(c\) 的值,然后求解其余系数
二次函数 \(f(x)=ax^2+bx+c\) 经过点 \((-2,-3)\), \((0,3)\) 和 \((4,3)\) 。求 \(a,b,c\) 的值。
解: 根据过点 \((0,3)\) 的条件,得到 \(c=3\) 及 \(f(x)=ax^2+bx+3\) 。

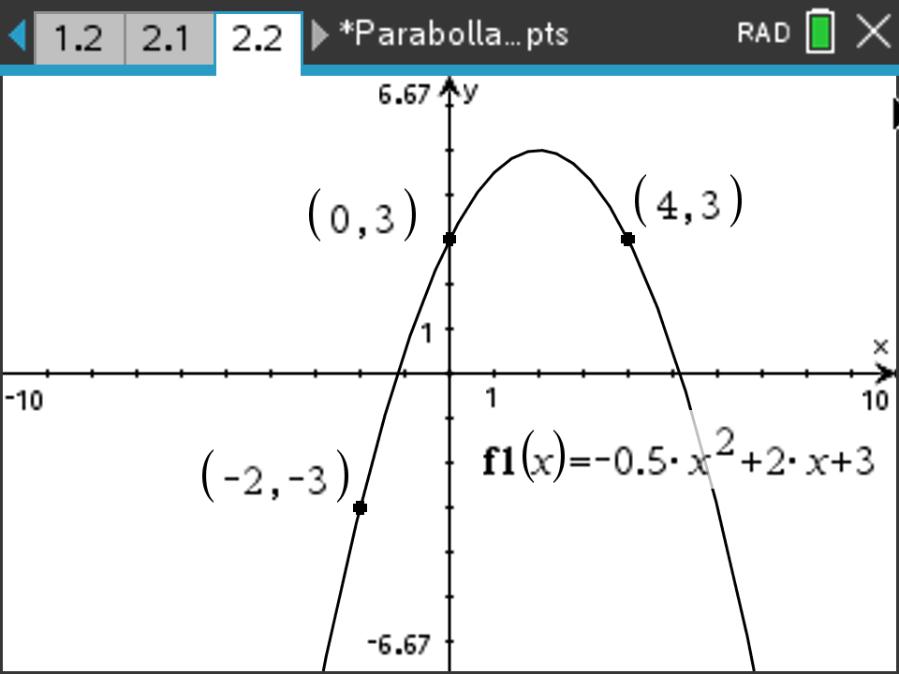
将其余两个点的坐标代入二次函数:
\(\begin{cases} f(-2)=-3\\ f(4)=3\end{cases}\) 得到: \(\begin{cases} 4a-2b=-6\\ 16a+4b=0\end{cases}\)
解得:\(\begin{cases} a=-\dfrac{1}{2}\\ b=2\end{cases}\)
因此二次函数为 \(f(x)=-\dfrac{1}{2}x^2+2x+3\)☐
利用截距简化方程组
在 \(f(x)=ax+bx+c\) 中,\(c\) 为图像在 \(y\) 轴上的截距。有时候题目会直接给出截距,从而简化计算。这是直接得到 \(c\) 的值,只需要列二元一次方程求解即可。
示例: 二次函数 \(f(x)=x^2+bx+c\) 在 \(y\) 轴的截距为 \(3\) ,且经过点 \((1,4)\) ,求 \(b,c\) 的值。
示例: \(f(x)=mx^2+mx+2m+1\) 经过点 \((1,9)\) ,求 \(m\) 的值。
二次函数的顶点式
在获得关于顶点、对称轴等关键信息时,往往采用顶点式可以简化计算。二次函数的顶点式为:\[f(x)=a(x-h)^2+k,\ \ a\neq0\]
顶点坐标为 \((h,k)\) ,对称轴为 \(x=h\) 。
请注意,如果条件明确指定了顶点的坐标,相当于确定了二次函数三个自由度中的两个。
示例: 二次函数 \(f(x)=ax^2+bx+c\) 的顶点为 \((3,3)\) ,\(y\) 轴截距为 \(-1\) ,求 \(a,b,c\) 的值。
二次函数的最值问题
二次函数在全数轴上的最值
二次函数 \(f(x)=ax^2+bx+c,a\neq0\) 在对称轴 \(x=-\dfrac{b}{2a}\) 处,也即顶点处,取到最值。
如果二次函数开口向上 \(a>0\) ,则为最小值。如果二次函数开口向下,则为最大值。
示例: 利用对称轴坐标求二次函数最值
求函数 \(f(x)=2x^2+4x-12\) 的最值。
解: 函数开口向上,所以在对称轴 \(x=-\dfrac{b}{2a}=-1\) 处取得最小值 \(f(-1)=-14\)。☐
示例: 利用配方法求二次函数最值
求函数 \(f(x)=2x^2+4x-12\) 的最值。
解: \(f(x)=2(x+1)^2-14\) ,当 \(x=-1\) 时取到最小值 \(-14\) 。☐
在含有字母系数,尤其是 \(x^2\) 项的系数含有字母时,要注意分类讨论。特别是要注意二次函数退化为直线时的情形。
示例: 根据字母系数分情况讨论函数最值
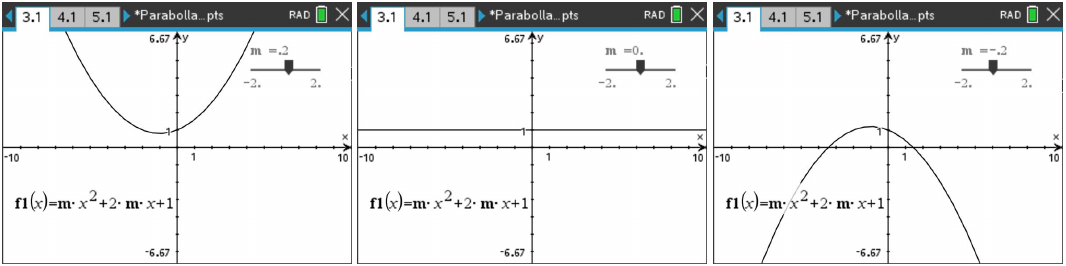
求函数 \(f(x)=mx^2+2mx+1\) 的最大值。
解: 诸如此类问题,要细心分类讨论:
当 \(m=0\) 时,函数变为常函数 \(f(x)=1\) ,最大值即为 \(0\) 。
当 \(m>0\) 时,图像开口向上,函数无最大值。
当 \(m<0\) 时,图像开口向下,在 \(x=-\dfrac{2m}{m}=2\) 时取到最大值 \(8m+1\) 。☐
二次函数在区间上的最值
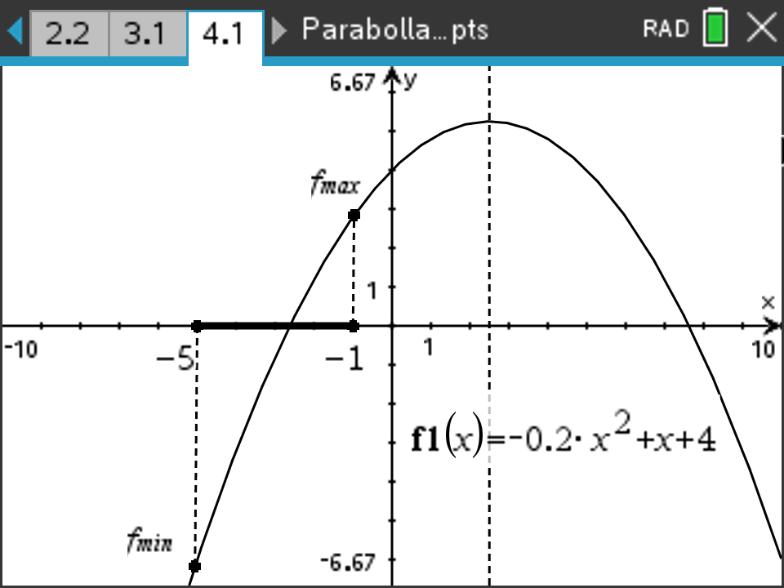
二次函数在区间内的最值出现在区间端点,
示例: 求 \(f(x)=-\dfrac{1}{5}x^2+x+4\) 在 \(-5\leq x\leq-1\) 时的最值。
示例: 求 \(f(x)=-\dfrac{1}{5}x^2+x+4\) 在 \(1\leq x\leq6\) 时的最值。
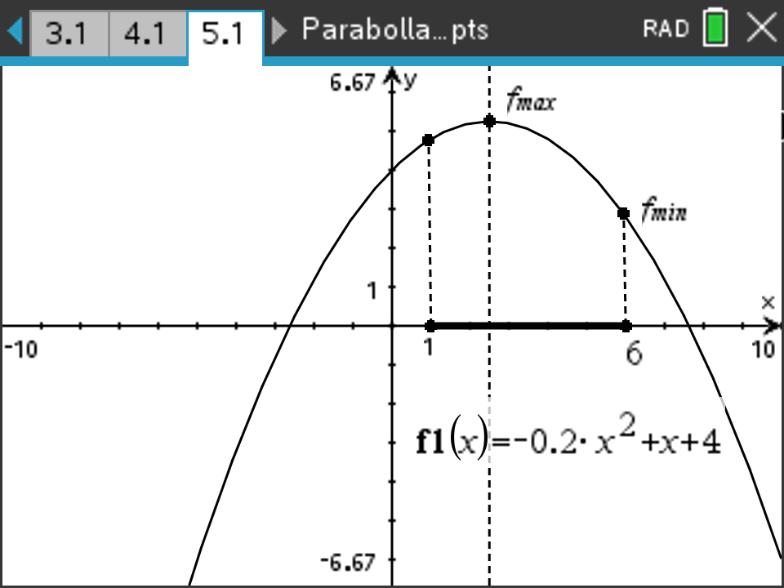
示例: 求 \(f(x)=\dfrac{1}{2}x^2+3x-3\) 在 \(-5\leq x\leq5\) 时的最值。
示例: 求 \(f(x)=\dfrac{1}{2}x^2+3x-3\) 在 \(-10\leq x\leq10\) 时的最值。
示例: 含有字母系数的二次函数在区间上的最值
已知函数 \(f(x,m)=3x^2-6mx+1\)
在 \(1\leq x\leq2\) 时,讨论函数的最值。
若函数在 \(1\leq x\leq2\) 时最小值为 \(-2\) ,求 \(m\) 的值。
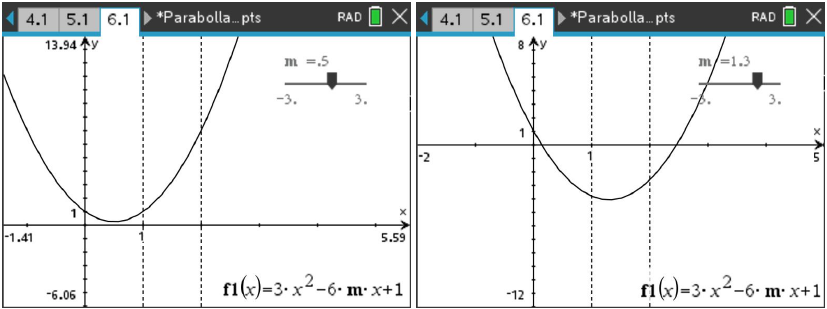
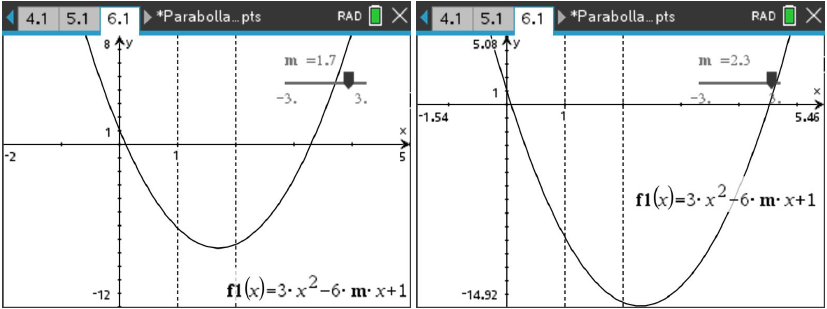
解: (1) 图像对称轴为 \(x=m\) ,分情况讨论:(如图 8 与 )

- 函数的最小值随 \(m\) 的变化是一个分段函数 \[f_{min}(m)= \begin{cases} 4-6m,\ \qquad m<1\\ -3m^2+1,\ \quad1\leq m\leq2\\ 13-12m,\quad\ \ 2<m\end{cases}\]
☐
示例:1 从直角三角形 \(ABC\) 的斜边 \(BC\) 上的一点 \(P\) ,做 \(AB,AC\) 的垂线,设垂足分别是 \(Q\) 和 \(R\) 。当 \(P\) 在什么位置时,矩形 \(AQPR\) 的面积最大?(提示:建立坐标系)
示例:2 先利用 \(m\) 表示函数 \(y=x^2-2mx+2m^2-m+1\) 的最小值;然后求当 \(m\) 取什么值时,\(y\) 取最小值中的最小值。
示例:3 当 \(x=3\) 时, \(x\) 的二次函数 \(y=ax^2+bx+\dfrac{1}{4a}\) 取最大值 \(m\) ;而当 \(x=1\) 时,函数值为 \(-2\) 。求 \(a,b,m\) 的值。
示例:4 有一个 \(x\) 的二次式,当 \(x=3\) 时取最大值 \(10\) ,并且它的图像在 \(x\) 轴上截得的线段长为 \(4\) 。求这个二次式。
示例: \(t\leq x\leq t+1\) 时,求 \(\dfrac{1}{2}x^2-x-\dfrac{5}{2}\) 的最小值。
示例: 解关于 \(x\) 的不等式 \(ax^2-(a+1)x+1<0\)
示例: 求 \(x^2+|x-a|+1\) 的最小值。
示例: 设 \(x\) 的函数 \(f(x)=ax^2-2x+2\) ( \(a\) 为常数)对于满足 \(1<x<4\) 的一切 \(x\) 值都有 \(f(x)>0\) ,求常数 \(a\) 值的范围。
示例: 铅锤最值:当一次函数与二次函数相交时,如图所示为 \(y=x^2\) 与 \(y=x+1\) ;
在相交区域中,竖直长度有一个最大值 \(\_\_\_\_\_\_\) 。
假设两个交点为 \(A,B\) ,同时在二次函数这段弧上有一个点 \(D\) 使得 \(\triangle{ABD}\) 面积最大。
\(D\) 应为 \(\_\_\_\_\_\_\) ,面积最大值为 \(\_\_\_\_\_\_\) 。
将 \(y=x+1\) 改为 \(y=x+2\) ,此时 \(D\) 应为 \(\_\_\_\_\_\_\) ,面积最大值为 \(\_\_\_\_\_\_\) 。
分析 \(D\) 的坐标与 \(A,B\) 坐标,你可以得到什么结论?
示例: 已知二次函数 \(y=\dfrac{1}{2}x^2+bx+1\) 。
若 \(b=-1\) ,求该二次函数图像的对称轴及最小值;
若对于任意的 \(0\leq x\leq2\) 都有 \(y\geq-1\) ,求 \(b\) 的取值范围。
函数(方程)图像的变换
图像的平移变换
方程 \(f(x,y)=0\) 的图像向右平移 \(a\) ,向上平移 \(b\) 个单位长度后得到的函数为 \(f(x-a,y-b)\)
示例: 对二次函数进行平移操作
将 \(y=x^2\) 的图像向右平移两个单位长度,向下平移三个单位长度。写出新图像的函数方程并绘制图像。
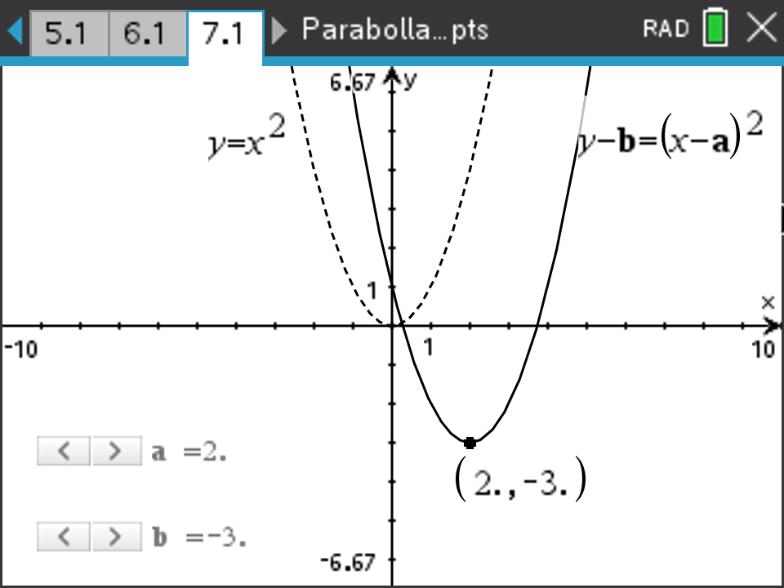
解: \(y=x^2\) 平移操作的模板为 \((y-b)=(x-a)^2\)。
根据平移要求 \(a=2,b=-3\) ,得到新的方程为:\[y+3=(x-2)^2\] \[y=(x-2)^2-3\]
整理得到 \(y=x^2-4x+1\),图像如图 11 所示。☐
图像的缩放变换
方程 \(f(x,y)=0\) 的图像在 \(x\)方向上放大为原来的 \(a\) 倍 ,在 \(y\) 方向上放大为原来的 \(b\) 倍后得到的函数为 \(f\left(\dfrac{x}{a},\dfrac{y}{b}\right)\)
示例: 对二次函数进行缩放操作
将 \(y=x^2+x-1\) 的图像在 \(x\) 方向上放大为原来的三倍,在 \(y\) 方向上放大为原来的两倍。写出新图像的函数方程并绘制图像。
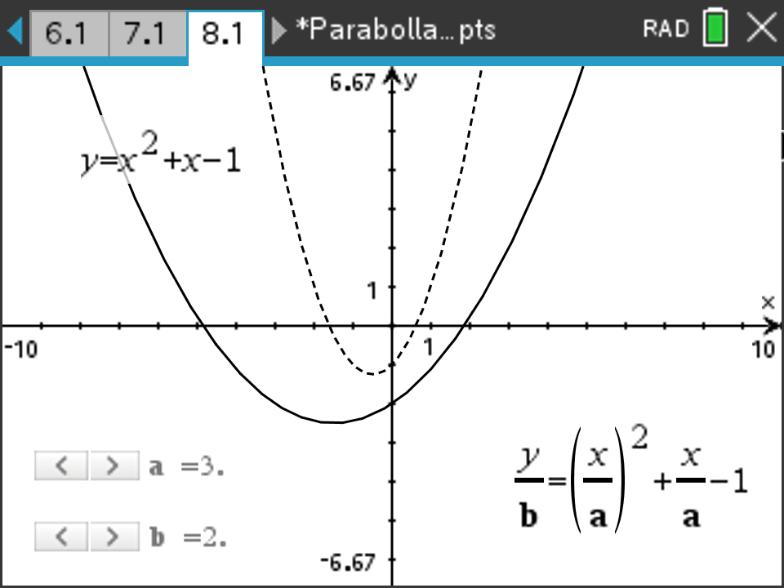
解: \(y=x^2+x-1\) 平移操作的模板为 \(\dfrac{y}{b}=\left(\dfrac{x}{a}\right)^2+\dfrac{x}{a}-1\)。
根据缩放要求 \(a=3,b=2\) ,得到新的方程为:\[\dfrac{y}{2}=\left(\dfrac{x}{3}\right)^2+\dfrac{x}{3}-1\]
整理得到 \(y=\dfrac{2}{9}x^2+\dfrac{2}{3}x-2\) ,图像如图 13 所示。☐
思考与讨论
- 向正方向移动就要减去位移,放大就要除以倍数,为什么?
- 这里讨论的“方程图像”和“函数图像”有什么同异?
根的存在性和韦达定理
二次函数的零点/一元二次方程的根
二次函数 \(f(x)=ax^2+bx+c,\ a\neq0\) 的零点就是 \(f(x)=0\) 时 \(x\) 的取值。也即方程 \(ax^2+bx+c=0,\ a\neq0\) 的根。
判别式 \(\Delta=b^2-4ac\) 用来判断零点的存在性。
\(\Delta<0\) 时 ,二次函数没有零点;
\(\Delta=0\) 时,二次函数和 \(x\) 轴相切,有一个零点(顶点)。
\(\Delta>0\) 时,二次函数和 \(x\) 轴相交,有两个零点。
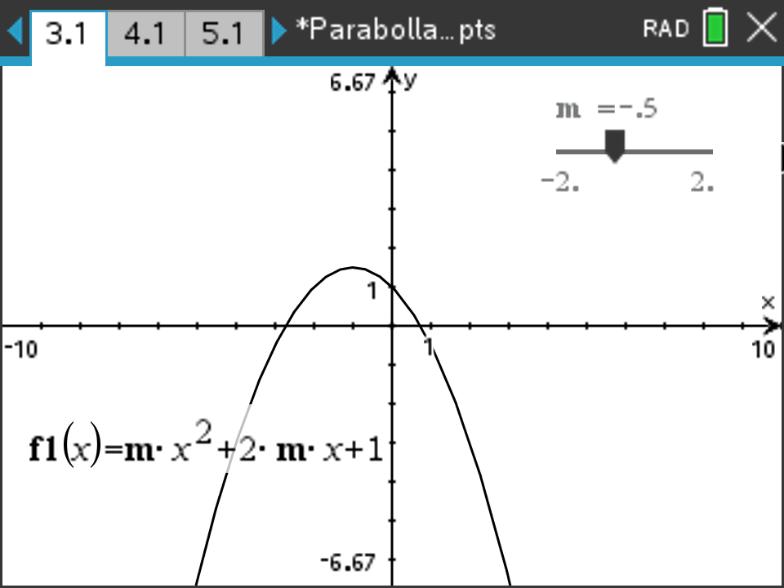
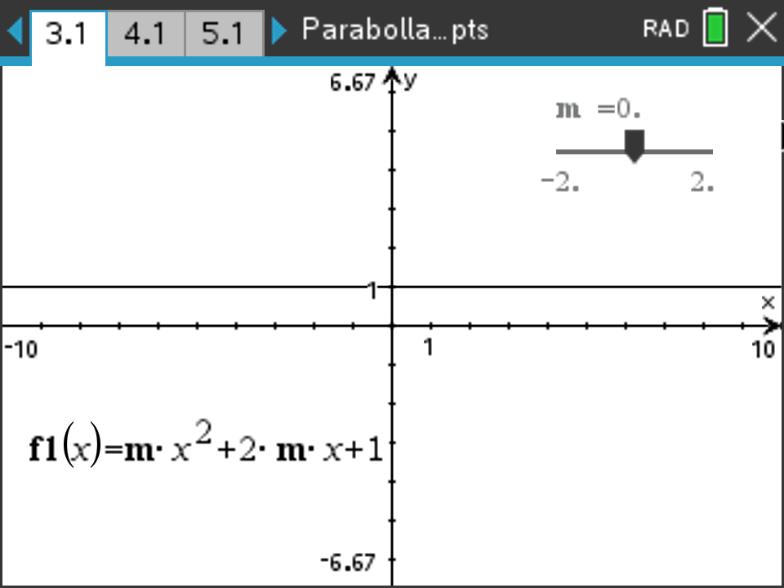
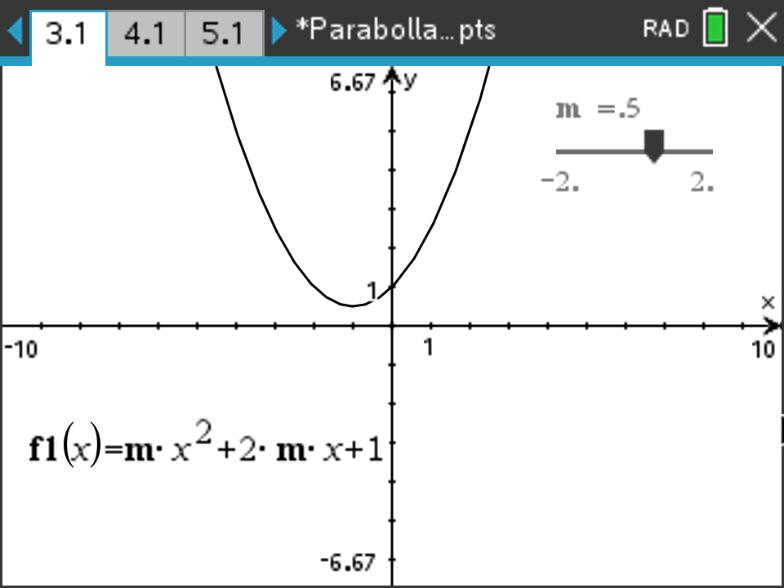
示例: 讨论二次函数的零点个数
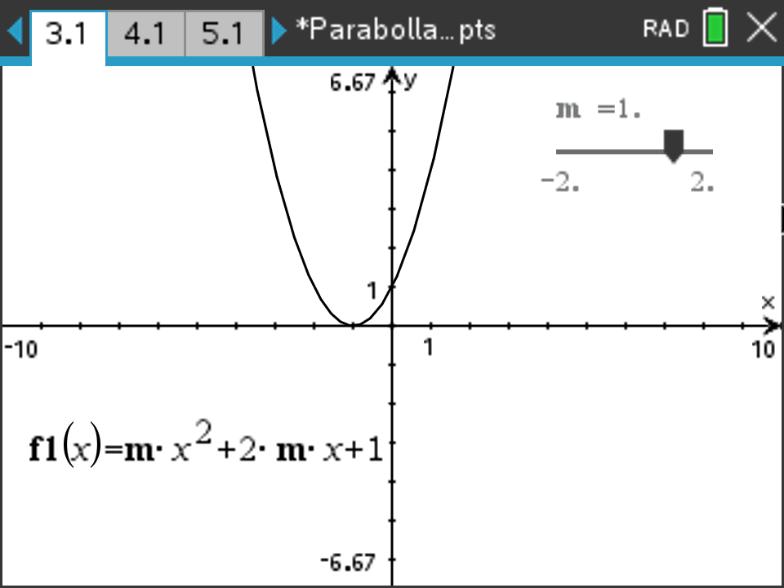
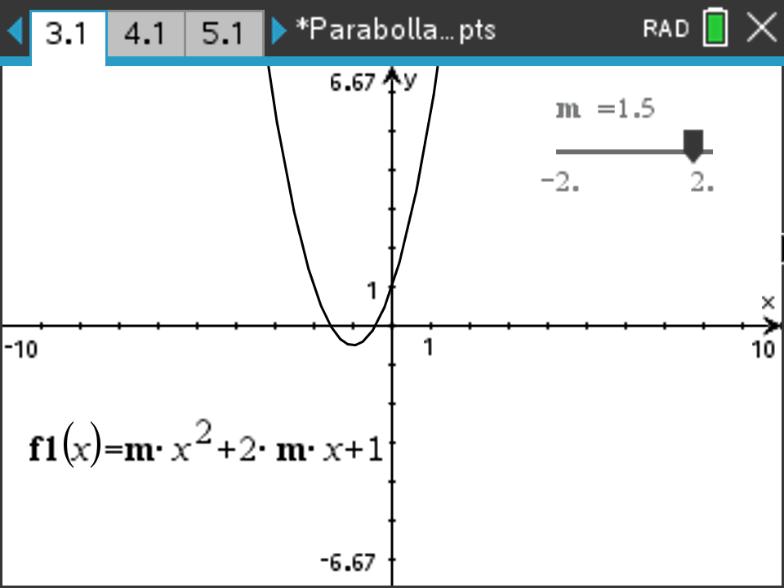
讨论 \(f(x)=mx^2+2mx+1\) 的零点个数与 \(m\) 的关系。
分析 要特别注意判别式的使用条件是二次项的系数不为 \(0\) 。
当二次项系数为 \(0\) ,函数图像退化为直线,一般来说容易处理。
当二次项系数不为 \(0\) 时,讨论判别式 \(\Delta\) 的符号,解不等式即可。
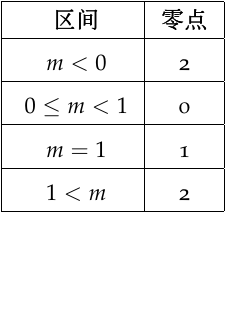
解: 当 \(m=0\) 时,函数退化为常函数 \(f(x)=1\) 无零点。
当 \(m\neq0\) 时,可以使用判别式:\[\Delta=4m^2-4m,\ m\neq0\]
\(\Delta=0,\ m\neq0\ \ \Leftrightarrow\ \ m=1\) ,函数有一个零点
\(\Delta>0,\ m\neq0\ \ \Leftrightarrow\ \ m>1\ or\ m<0\) ,函数有两个零点
\(\Delta>0,\ m\neq0\ \ \Leftrightarrow\ \ 0<m<1\) ,函数没有零点
综上所述得到下表。☐
一元二次方程根与系数的关系
定理: 韦达定理 对于一元二次方程 \[ax^2+bx+c=0,\ a\neq0\] 两根 \(x_1,x_2\) 有如下关系:\[x_1+x_2=-\dfrac{b}{a},\ \ x_1x_2=\dfrac{c}{a}\]
——百度百科《韦达定理》词条
示例: 已知 \(x_1,x_2\) 是方程 \(2x^2+3x-4=0\) 的两个根,求
(1). \(\dfrac{1}{x_1}+\dfrac{1}{x_2}\) (2). \(x_1^2+x_2^2\) (3). \((x_1+1)(x_2+1)\) (4). \(|x_1-x_2|\)
分析 可以直接求得两根 \(x_{1,2}=-\dfrac{1}{4}\left(3\pm\sqrt{41}\right)\) 后计算,但计算量巨大。注意到所求的表达式均为对称式,容易写成 \(s=x_1+x_2\) 和 \(p=x_1x_2\) 的表达式。利用韦达定理可以直接得到 \(x_1+x_2\) 和 \(x_1x_2\) 的值,进而简化计算。
解: 根据韦达定理,\(s=x_1+x_2=-\dfrac{3}{2}\) , \(p=x_1x_2=-2\)
(1). \(\dfrac{1}{x_1}+\dfrac{1}{x_2}=\dfrac{s}{p}=\dfrac{3}{4}\)
(2). \(x_1^2+x_2^2=s^2-2p=\dfrac{25}{4}\)
(3). \((x_1+1)(x_2+1)=s+p+1=-\dfrac{5}{2}\)
(4). \(|x_1-x_2|=\sqrt{s^2-4p}=\dfrac{\sqrt{41}}{2}\)☐
示例: 关于 \(x\) 的方程 \(x^2-3x+k=0\) 两根立方和为 \(0\) ,求 \(k\) 。
示例: 利用韦达定理处理两根之比问题
求证:命题A “\(ax^2+bx+c=0,a\neq0\) 的两根之比为 \(\dfrac{2}{3}\)” 等价于
\(\quad\)命题B “\(6b^2=25ac\) 且 \(abc\neq0\)” 。
分析 这里的关键技巧就是构建 \(\dfrac{x_1}{x_2}+\dfrac{x_2}{x_1}\)
证明 证等价性,要分别从充分性和必要性加以证明。
先证 \(A\Rightarrow B\) :
易证 \(b\neq0\) 且 \(c\neq0\) ,故 \(abc\neq0\) 。否则两根绝对值相等或有一根为 \(0\) ,无法形成所要求的比例
不妨令两根为 \(x_1,x_2\) ,则 \(\dfrac{x_1}{x_2}+\dfrac{x_2}{x_1}=\dfrac{2}{3}+\dfrac{3}{2}=\dfrac{13}{6}\)
又\(\because\) \(\dfrac{x_1}{x_2}+\dfrac{x_2}{x_1}=\dfrac{(x_1+x_2)^2-2x_1x_2}{x_1x_2}\)
\(\therefore\) \((x_1+x_2)^2-2x_1x_2=\dfrac{13}{6}x_1x_2\) ,即 \(\left(-\dfrac{b}{a}\right)^2-2\dfrac{c}{a}=\dfrac{13}{6}\cdot\dfrac{c}{a}\)
整理得 \(6b^2=25ac\)
再证 \(B\Rightarrow A\) :
\(\because\) \(ac=\dfrac{6}{25}b^2\) 得到:
\(\therefore\) \(\Delta=b^2-4ac=\dfrac{b^2}{25}>0\) ,方程存在两个根。
\(\because\) \(6b^2=25ac\) 且 \(abc\neq0\)
\(\therefore\) \(\left(-\dfrac{b}{a}\right)^2-2\dfrac{c}{a}=\dfrac{13}{6}\cdot\dfrac{c}{a}\)
\(\therefore\) \((x_1+x_2)^2-2x_1x_2=\dfrac{13}{6}x_1x_2\)
\(\therefore\) \(\dfrac{x_1}{x_2}+\dfrac{x_2}{x_1}=\dfrac{13}{6}\)
令 \(\dfrac{x_1}{x_2}=t\) 得到 \(t+\dfrac{1}{t}=\dfrac{13}{6}\)
解得 \(t=\dfrac{2}{3}\) 或 \(t=\dfrac{3}{2}\) ,即两根之比为 \(\dfrac{2}{3}\) 。
综上所述, \(A\Leftrightarrow B\) 。☐
二次函数图像与直线的关系问题
二次函数图像与直线的交点,可通过连立二次方程和线性方程得到。在具体问题中,可以使用判别式确定二者的交点个数,也可以使用韦达定理确定相交弦的中点等信息。
示例: 判定抛物线和直线的交点个数
讨论 \(y=\dfrac{1}{2}x^2-2\) 与 \(y=x+b\) 的交点个数与 \(b\) 的关系。

解: 联立抛物线和直线的方程,并消去 \(y\) :
\[\begin{cases} y=\dfrac{1}{2}x^2-2\\ y=x+b\end{cases}\Rightarrow \dfrac{1}{2}x^2-x-(b+2)=0\]
判别式 \(\Delta=5+2b\) 。
\(\Delta>0\) 即 \(b>-\dfrac{5}{2}\) 时,抛物线和直线有两个交点。
\(\Delta=0\) 即 \(b=-\dfrac{5}{2}\) 时,抛物线和直线有一个交点。
\(\Delta<0\) 即 \(b<-\dfrac{5}{2}\) 时,抛物线和直线无交点。☐
示例: 求二次函数在一点处的切线方程
求 \(y=x^2\) 在 \((2,4)\) 点处的切线方程。
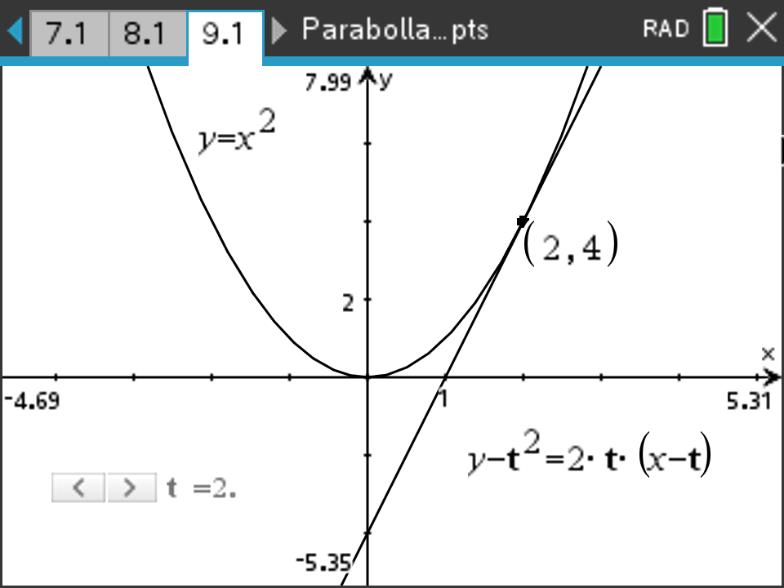
解: 显然直线不竖直,所以斜率存在。设切线方程的斜率为 \(k\) ,则直线的点斜式方程为 \(y-4=k(x-2)\) 联立得到方程组并消去 \(y\) :
\[\begin{cases} y=kx-2k+4\\y=x^2\end{cases}\Rightarrow x^2-kx+2k-4=0\]
根据相切条件,上述二元一次方程的判别式为 \(0\) :\[\Delta=k^2-8x+16=0\]
得到 \(k=4\) ,因此所求之切线方程为 \(y=4x-4\) 。☐
示例: 求抛物线和直线相交弦的中点
求抛物线 \(y=\dfrac{1}{2}x^2-2\) 和 \(y=mx\) 相交弦的中点坐标。
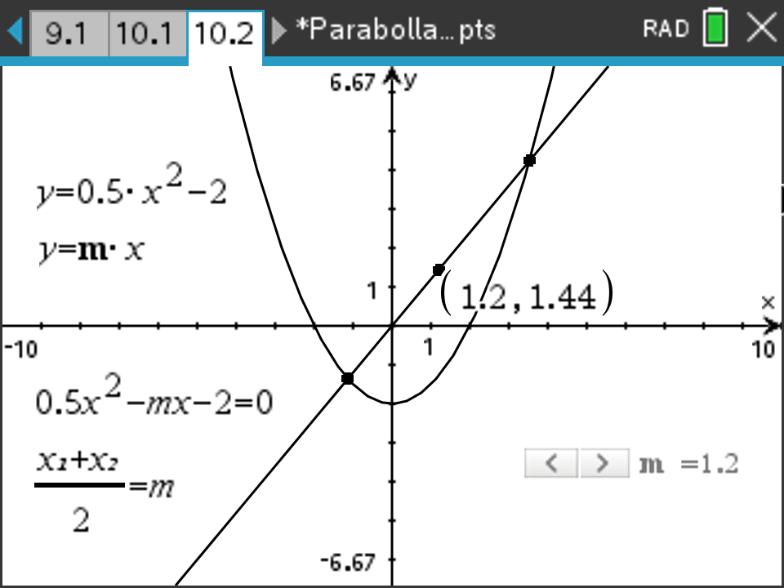
解: 联立抛物线和直线的方程,并消去 \(y\) :
\[\begin{cases} y=\dfrac{1}{2}x^2-2\\ y=mx\end{cases}\Rightarrow \dfrac{1}{2}x^2-mx-2=0\]
两个根 \(x_1,x_2\) 就是相交弦端点的横坐标。
根据韦达定理,中点的横坐标为 \(\dfrac{x_1+x_2}{2}=m\) 。
代入直线方程,得到相交弦的中点坐标为:\((m,m^2)\) 。☐
使用判别式求函数值域
有时在求函数值域时,可以将函数值设为一个参数,然后整理为二次方程,再利用判别式“反戈一击”。这是在学习三角函数换元、解析几何和微积分技巧之前的一种常用手段。
示例: 求二次函数的值域
求二次函数 \(f(x)=x^2+x-2\) 的值域。
解: \(f(x)\) 的值域就是让方程 \(f(x)=a\) 有解的 \(a\) 的取值范围。另一个方法是直接计算顶点的坐标,从而求得值域。
整理方程得:\(x^2+x-(a+2)=0\)
计算判别式:\(\Delta=4a+9\geq0\) ,得到 \(a\geq-\dfrac{9}{4}\)
因此 \(f(x)\) 的值域就是 \(\left[-\dfrac{9}{4},+\infty\right)\)☐
此处看似舍近求远,然目的是让读者熟悉这一方法,进而将其用于更复杂的问题。
示例: 求可以转换为二次函数的根式函数的值域
5 求 \(f(x)=2\sqrt{x^2+1}+x\) 的值域。
解: 设 \(a=2\sqrt{x^2+1}+x\)
\(a-x=2\sqrt{x^2+1}\) 两边平方得:
\((a-x)^2=4(x^2+1)\) 其中 \(x\leq a\) 。整理得:
\(3x^2+2ax+4-a^2=0, \ x\leq a\)
根据题意,该方程在 \((-\infty,a]\) 区间内有根小心求解 \(\dfrac{-2a-\sqrt{16a^2-48}}{6}\leq a\)
\[\begin{equation*} \begin{cases} \Delta=16a^2-48\geq0\\ \\ \dfrac{-2a-\sqrt{16a^2-48}}{6}\leq a \end{cases} \Leftrightarrow \begin{cases} a\leq-\sqrt{3}\ or\ a\geq\sqrt{3}\\ \\ a\geq0 \end{cases} \Leftrightarrow a\geq\sqrt{3} \end{equation*}\]
因此 \(f(x)\) 的值域为 \([\sqrt{3},+ \infty)\) 。☐
判别式法有时候的计算量很大,也不容易看出直观的意义。随着学习的深入,这类问题往往有其它更好的方法。
基础习题
练习: 已知二次函数 \(f(x)=ax^2+bx+c\) 经过点 \((-2,9),(-1,2),(1,6)\) ,求 \(a,b,c\) 的值。
练习: 已知二次函数 \(f(x)=ax^2+bx+c\) 经过点 \((-2,4),(0,2),(1,7)\) ,求 \(a,b,c\) 的值。
练习: 已知二次函数 \(f(x)=ax^2+bx+c\) 的顶点为 \((4,3)\) ,还经过点 \((1,2)\) ,求 \(a,b,c\) 的值。
练习: 已知二次函数的对称轴为 \(x=1\) ,\(y\) 轴截距为 \(2\) ,与 \(x\) 轴的一个交点的横坐标为 \(4\) ,求二次函数的表达式。
练习: \(\bigstar\) 求函数 \(f(x)=mx^2-3mx+3\) 在区间 \(0\leq x\leq2\) 上的最值。
练习: 写出 \(y=2x^2+x+1\) 的图像向下移动三个单位长度后的图像方程(整理成标准式),并用计算器绘图验证。
练习: 写出 \(y=x+\dfrac{1}{x}\) 在 \(x\) 方向上压缩为 \(\dfrac{1}{2}\) 后的图像方程,并用计算器绘图验证。
练习: 写出 \(x^2+y^2=1\) 在 \(y\) 方向上拉伸为原来两倍后的图像方程,并用计算器绘图验证。
练习: \(\bigstar\) \(y=2x^2+x+1\) 做什么样的变换后能与 \(y=x^2\) 重合。
练习: 已知一元二次方程 \(2x^2-3x-1=0\) 的两根为 \(x_1,x_2\) ,利用根与系数的关系,求下列表达式的值。
(1). \(x_1^3x_2+x_1x_2^3\) (2). \(\dfrac{1}{x_1^2}+\dfrac{1}{x_2^2}\) (3). \((x_1^2-x_2^2)^2\)
(4). \(x_1-x_2\) (5). \(\dfrac{x_2^2}{x_1}+\dfrac{x_1^2}{x_2}\) (6). \(x_1^5x_2^2+x_1^2+x_2^5\)
练习: 抛物线 \(y=x^2\) 与过点 \((2,-1)\) 的直线恰有一个公共点,求所有可能的直线。
练习: 求抛物线的 \(y=x^2\) 与直线 \(y=2x+5\) 相交弦的长度及中点坐标。
练习: 用判别式法求 \(f(x)=\dfrac{x^2+x+1}{x+1}\) 的值域。
练习: 用换元法求 \(f(x)=\dfrac{x^2+x+1}{x+1}\) 的值域。
练习: 在平面直角坐标系 \(xOy\) 中,过点 \((0,2)\) 且平行于 \(x\) 轴的直线,与直线 \(y=x﹣1\) 交于点 \(A\) ,点 \(A\) 关于直线 \(x=1\) 的对称点为 \(B\) ,抛物线 \(C1:y=x^2+bx+c\) 经过点 \(A\),\(B\) 。
- [(1)] 求点 \(A\),\(B\) 的坐标;
- [(2)] 求抛物线 \(C1\) 的表达式及顶点坐标;
- [(3)] 若抛物线 \(C2:y=ax^2\ \ (a\neq0)\) 与线段 \(AB\) 恰有一个公共点,结合函数的图象,求 \(a\) 的取值范围。